题目内容
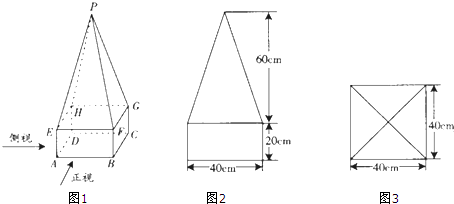
某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是侧面全等的四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图2、图3分别是该标识墩的正(主)视图和俯视图.
(1)求该安全标识墩的体积;
(2)现在需要在安全标识墩的表面(底面不涂)涂上反光材料,每100cm2需要反光涂料0.015千克,请问需要多少千克涂料?(参考值
≈3.162,结果保留两位小数)
(1)求该安全标识墩的体积;
(2)现在需要在安全标识墩的表面(底面不涂)涂上反光材料,每100cm2需要反光涂料0.015千克,请问需要多少千克涂料?(参考值
| 10 |

考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(1)由三视图我们易得,底面为边长为40cm的正方形,长方体的高为20cm,棱锥高为60cm,代入棱柱和棱锥体积公式,易得结果.
(2)先求出该安全标识墩的侧面积,再求需用油漆量.
(2)先求出该安全标识墩的侧面积,再求需用油漆量.
解答:
解:(Ⅰ)由三视图我们易得,底面为边长为40cm的正方形,长方体的高为20cm,棱锥高为60cm,
∴该安全标识墩的体积为:V=VP-EFGH+VABCD-EFGH
=
×40×40×60+40×40×20
=64000(cm3).…(6分)
(Ⅱ)∵该安全标识墩的上半部分是正四棱锥P-EFGH,
EFGH边长为40cm的正方形,正四棱锥P-EFGH的高为60cm,
∴正四棱锥P-EFGH的斜高为20
,
下半部分是长、宽、高分别为40cm,40cm,20cm的长方体ABCD-EFGH,
∴该安全标识墩的侧面积:
S=(20×40+
×40×20
)×4=800(4+2
)(cm2),
∴涂料8(4+2
)×0.015=1.24 千克
∴该安全标识墩的体积为:V=VP-EFGH+VABCD-EFGH
=
| 1 |
| 3 |
=64000(cm3).…(6分)
(Ⅱ)∵该安全标识墩的上半部分是正四棱锥P-EFGH,
EFGH边长为40cm的正方形,正四棱锥P-EFGH的高为60cm,
∴正四棱锥P-EFGH的斜高为20
| 10 |
下半部分是长、宽、高分别为40cm,40cm,20cm的长方体ABCD-EFGH,
∴该安全标识墩的侧面积:
S=(20×40+
| 1 |
| 2 |
| 10 |
| 10 |
∴涂料8(4+2
| 10 |
点评:本题考查考查组合体的侧面积、体积的求法及应用,处理的关键是准确判断空间几何体的形状.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,两块斜边长相等的直角三角板拼在一起,若
如图,两块斜边长相等的直角三角板拼在一起,若