题目内容

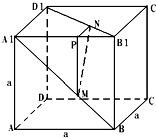在棱长为a的正方体ABCD-A1B1C1D1中，M、N、P分别为边A1B、B1D1、A1B1上的点，若
B1N
B1D1
=
BM
BA1
=
2
5
，求证：MN∥平面AA1D1D．
考点：直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：过N在平面B1D1内，作NP∥A1D1，交A1B1于P，连接PM，由平行线分线段成比例的判定和性质，得到PM∥AA1，再由线面平行的判定定理，证得PM∥平面ADD1A1，PN∥平面ADD1A1，再由面面平行的判定定理得到平面PMN∥平面ADD1A1，再由面面平行的性质即可得到MN∥平面AA1D1D．
解答： 证明：过N在平面B1D1内，作NP∥A1D1，交A1B1于P，连接PM，
则
B1N
ND1
=
B1P
PA1
=
2
3
，
由于
B1N
ND1
=
BM
MA1
=
2
3
，
则
B1P
PA1
=
BM
MA1
，
即有PM∥B1B，
又B1B∥A1A，则PM∥AA1，
由于PM?平面ADD1A1，A1A?平面ADD1A1，
则PM∥平面ADD1A1，
同理可得PN∥平面ADD1A1，
由PN∩PM=P，则平面PMN∥平面ADD1A1，
由于MN?平面PMN，则MN∥平面AA1D1D．
点评：本题考查直线与平面的判定，考查运用面面平行的性质证明线面平行的方法，关键是先找到两平行平面，注意运用平面几何的平行知识，属于中档题．
练习册系列答案
相关题目
若使得方程
16-x2
-x-m=0有实数解，则实数m的取值范围为（　　）
A、-4
2
≤m≤4
2
B、-4≤m≤4
2
C、-4≤m≤4
D、4≤m≤4
2
若t2+4t＜mt，t∈[1，4]，求m的取值范围．
双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线均与x2+y2-4x+1=0相切，则该双曲线离心率等于
 
．
已知a，b为两异面直线，OA∥a，OB∥b，若∠AOB=150°，则a，b所成的角为
 
．
已知首项a1=1各项都是正数的数列{an}（n∈N*），使目标函数z=3x+2y在约束条件
y≤anx
7x+2y≤2an+1
y≥-1
下最大值为2（an+1）2．
（1）求an与an+1的关系；
（2）证明：bn=
2an-1
an+3
是等比数列；
（3）证明：
n+1
2
≤a1+a2+…+an≤
n+2
2
．
已知椭圆C：
y2
a2
+
x2
b2
=1（a＞b＞0）经过点(
3
2
，1)，一个焦点是F（0，1）．
（1）求椭圆C的方程；
（2）若倾斜角为
π
4
的直线l与椭圆C交于A、B两点，且|AB|=
12
2
7
，求直线l的方程．
在△ABC中，求证：
a-ccosB
b-ccosA
=
sinB
sinA
．
已知直线a，b，c，d，给出以下四个命题：
①若a∥b，a⊥c，则b⊥c；
②若a⊥c，b⊥c，则a∥b；
③若a，b分别和异面直线c，d都相交，则a，b是异面直线；
④已知a，b是异面直线，若AB∥a，BC∥b，则∠ABC是异面直线a，b所成的角，
则以上命题中正确命题的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网