题目内容
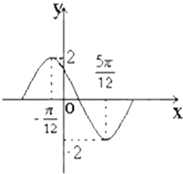 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)在一个周期内的图象如下
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)在一个周期内的图象如下(1)求函数的解析式;
(2)求函数的单调增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)直接由函数图象得到A和函数的半周期,由周期公式求得ω,再由五点作图的第二点求得φ,则函数解析式可求.
(2)根据正弦函数的单调性,构造不等式,解不等式可得函数的单调增区间.
(2)根据正弦函数的单调性,构造不等式,解不等式可得函数的单调增区间.
解答:
解:(1)由图可知,A=2,
=
-(-
)=
,
∴T=π,
又∵ω>0,
∴ω=2.
由五点作图的第二点得,2×(-
)+φ=
,
解得:φ=
.
∴函数解析式为:y=2sin(2x+
)
(2)由2x+
∈[-
+2kπ,
+2kπ](k∈Z)得:
x∈[-
+kπ,-
+kπ](k∈Z),
故函数的单调增区间为:[-
+kπ,-
+kπ](k∈Z)
| T |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| π |
| 2 |
∴T=π,
又∵ω>0,
∴ω=2.
由五点作图的第二点得,2×(-
| π |
| 12 |
| π |
| 2 |
解得:φ=
| 2π |
| 3 |
∴函数解析式为:y=2sin(2x+
| 2π |
| 3 |
(2)由2x+
| 2π |
| 3 |
| π |
| 2 |
| π |
| 2 |
x∈[-
| 7π |
| 12 |
| π |
| 12 |
故函数的单调增区间为:[-
| 7π |
| 12 |
| π |
| 12 |
点评:本题考查利用y=Asin(ωx+φ)的部分图象求函数解析式,关键是掌握运用五点作图的某一点求φ,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
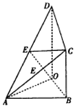 如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,
如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,