题目内容
解下列不等式:
(1)x2-(a+1)x+a<0(其中a≠1);
(2)
>x.
(1)x2-(a+1)x+a<0(其中a≠1);
(2)
| 2 |
| x-1 |
考点:其他不等式的解法,一元二次不等式的解法
专题:不等式的解法及应用
分析:本题(1)先将不等式左边进行因式分解,再进行分类讨论,比较出相应方程根的大小,得出结论;(2)先移项,再通分,然后转化不整式不等式求解,得到本题结论.
解答:
解:(1)∵x2-(a+1)x+a<0(其中a≠1),
∴(x-1)(x-a)<0,
当a<1时,原不等式的解集为(a,1);
当a>1时,原不等式的解集为(1,a).
(2)∵
>x,
∴
-x>0,
∴
>0,
∴
<0.
∴(x-1)(x-2)(x+1)<0.
∴x<-1或1<x<2,
即原不等式的解集为(-∞,-1)∪(1,2).
∴(x-1)(x-a)<0,
当a<1时,原不等式的解集为(a,1);
当a>1时,原不等式的解集为(1,a).
(2)∵
| 2 |
| x-1 |
∴
| 2 |
| x-1 |
∴
| 2-x2+x |
| x-1 |
∴
| (x-2)(x+1) |
| x-1 |
∴(x-1)(x-2)(x+1)<0.
∴x<-1或1<x<2,
即原不等式的解集为(-∞,-1)∪(1,2).
点评:本题考查了化归转化、分类讨论的数学思想,将分式不等式转化为整式不等式,分类讨论比较根的大小,本题有一定的难度和容量,属于中档题.

练习册系列答案
相关题目
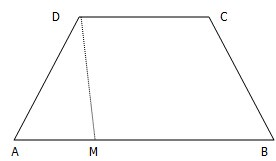 如图所示的四边形ABCD为等腰梯形,两腰与底边的夹角为45°,上底边长为2,高为2.点M从A点出发,沿梯形的边AB,BC运动,最后到达点C,若x表示点M的移动路程,S表示线段DM在四边形ABCD内部扫过的面积.
如图所示的四边形ABCD为等腰梯形,两腰与底边的夹角为45°,上底边长为2,高为2.点M从A点出发,沿梯形的边AB,BC运动,最后到达点C,若x表示点M的移动路程,S表示线段DM在四边形ABCD内部扫过的面积.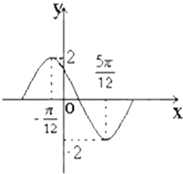 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)在一个周期内的图象如下
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)在一个周期内的图象如下
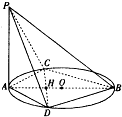 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.