题目内容
直线y=kx（k≠0）是曲线y=xex的切线，则k= ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出函数的导数，根据导数的几何意义即可得到结论．
解答：
解：函数的导数为y′=ex（x+1），设切点坐标为（a，aea），则切线方程为y-aea=ea（a+1）（x-a），
即y=ea（a+1）x-a2ea，
∵直线y=kx（k≠0）是曲线y=xex的切线，
∴k=ea（a+1）且a2ea=0，
解得a=0，则k=1，
故答案为：1．
即y=ea（a+1）x-a2ea，
∵直线y=kx（k≠0）是曲线y=xex的切线，
∴k=ea（a+1）且a2ea=0，
解得a=0，则k=1，
故答案为：1．
点评：本题主要考查导数的切线的求解和应用，根据导数的几何意义是解决本题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
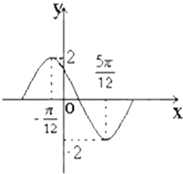函数y=Asin（ωx+ϕ）（其中A＞0，ω＞0，0＜ϕ＜π）在一个周期内的图象如下
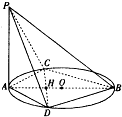已知AB是圆O的直径，C，D是圆上不同两点，且CD∩AB=H，AC=AD，PA⊥圆O所在平面．