题目内容
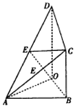 如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,
如图,△ABO是以AB为斜边的等腰直角三角形,OD⊥平面ABO,BC∥OD,且OD=2BC=2OA=2,E是AD中点,(Ⅰ)求证:CE∥平面ABO;
(Ⅱ)求三棱锥E-ABC的体积VE-ABC.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)取OA的中点F,连接BF,EF,先证明出四边形EFBC是平行四边形,进而推断出EC∥FB,根据线面平行的判定定理证明出EC∥平面ABO.
(Ⅱ)作AH⊥BF于H,先证明出平面EFBC⊥平面ABO,进而根据面面垂直的性质推断出AH⊥平面EFBC,分别求得OD,BC和OF,最后求得体积
(Ⅱ)作AH⊥BF于H,先证明出平面EFBC⊥平面ABO,进而根据面面垂直的性质推断出AH⊥平面EFBC,分别求得OD,BC和OF,最后求得体积
解答:
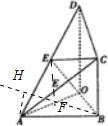
解:(Ⅰ)如图所示,取OA的中点F,连接BF,EF,
∵E是AD的中点,
∴EF∥OD,且EF=
OD,
又BC∥OD,且OD=2BC=2OA=2,
∴EF∥BC,且EF=BC,
∴四边形EFBC是平行四边形,
∴EC∥FB,又E?平面ABO,FB?平面ABO,
∴EC∥平面ABO.
(Ⅱ)如图,作AH⊥BF于H,由(Ⅰ)知,BC⊥平面ABO,BC?平面EFBC,
∴平面EFBC⊥平面ABO,
∴AH⊥平面EFBC,
∵OD=2BC=2OA=2,
∴BC=1.
OF=AF=
,CE=BF=
=
,由
=
,得AH=
.
∴VE-ABC=
×
×1×
×
=
.
∵E是AD的中点,
∴EF∥OD,且EF=
| 1 |
| 2 |
又BC∥OD,且OD=2BC=2OA=2,
∴EF∥BC,且EF=BC,
∴四边形EFBC是平行四边形,
∴EC∥FB,又E?平面ABO,FB?平面ABO,
∴EC∥平面ABO.
(Ⅱ)如图,作AH⊥BF于H,由(Ⅰ)知,BC⊥平面ABO,BC?平面EFBC,
∴平面EFBC⊥平面ABO,
∴AH⊥平面EFBC,
∵OD=2BC=2OA=2,
∴BC=1.
OF=AF=
| 1 |
| 2 |
1+
|
| ||
| 2 |
| AH |
| AF |
| OB |
| BF |
| ||
| 5 |
∴VE-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 5 |
| 1 |
| 12 |

点评:本题主要考查了线面平行的判定定理的应用.考查了学生空间观察和思维能力.

练习册系列答案
相关题目
对于函数f(x)=
的单调性表述正确的是( )
| 1-2x |
| x-1 |
| A、在(-∞,1)∪(1,+∞)上递增 |
| B、在(-∞,1)∪(1,+∞)上递减 |
| C、在(-∞,1),(1,+∞)上均递增 |
| D、在(-∞,1),(1,+∞)上均递减 |
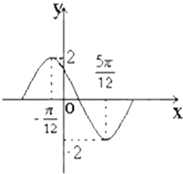 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)在一个周期内的图象如下
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)在一个周期内的图象如下