Question

设函数f（x）=a²lnx-x²+ax+b，已知a是正实数，若存在实数b，使得e≤f（x）≤e²+1对x∈[1，e]恒成立，试求a的取值范围．

Answer 1

考点：二次函数的性质

专题：函数的性质及应用,导数的概念及应用,导数的综合应用

分析：求出函数f（x）=a²lnx-x²+ax+b的二阶函数，分析函数的凸凹性，进而结合存在实数b，使得e≤f（x）≤e²+1对x∈[1，e]恒成立，可得

e≤f(1)≤e2+1 e≤f(e)≤e2+1

，画出满足约束条件的可行域，利用角点法，可求出a的取值范围．

解答： 解：∵f（x）=a²lnx-x²+ax+b，
∴f′（x）=a²•

1

x

-2x+a，
∴f″（x）=-a²•

1

x2

-2，
当x＞0时，f″（x）＜0恒成立，
故函数f（x）为凸函数，
若存在实数b，使得e≤f（x）≤e²+1对x∈[1，e]恒成立，
只需

e≤f(1)≤e2+1 e≤f(e)≤e2+1

即

e≤a+b-1≤e2+1 e≤a2-e2+ae+b≤e2+1

即

b≥-a+e+1 b≤-a+e2+2 b≥-a2-ea+e2+e b≤-a2-ea+2e2+1

满足约束条件的可行域如下图所示：

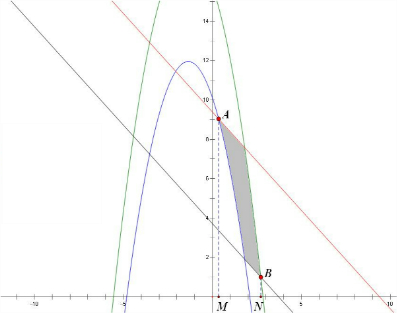
由

b=-a+e2+2 b=-a2-ea+e2+e

得a=

-e+1+ e2+2e-7

2

，或a=

-e+1- e2+2e-7

2

故M点的坐标为（

-e+1+ e2+2e-7

2

，0），
由

b=-a+e+1 b=-a2-ea+2e2+1

得a=e，或a=1-2e
故N点的坐标为N（e，0）
所以a的取值范围：

-e+1+ e2+2e-7

2

≤a≤e

点评：本题考查的知识点是导数法判断函数凸凹性，运算强度大，变形思路比较小，难度较大．