Question

已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），直线x-

3

y+

3

=0经过椭圆C的上顶点B和左焦点F，设椭圆右焦点为F′．
（Ⅰ）求椭圆C的标准方程；
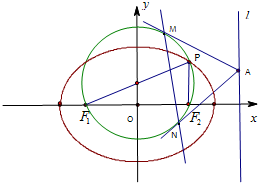
（Ⅱ）设P是椭圆C上动点，求|4-（|PF′|+|PB|）|的取值范围，并求取最小值时点P的坐标．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）由已知直线方程求得椭圆左焦点及上顶点的坐标，则b，c的值可求，结合a²=b²+c²求得a²，则椭圆方程可求；
（Ⅱ）利用椭圆定义，把|4-（|PF′|+|PB|）|转化为||PF|-|PB||，得到||PF|-|PB||的取值范围，然后求出||PF|-|PB||取最小值时的P的轨迹，和椭圆方程联立求得P的坐标．

解答： 解：（Ⅰ）由x-

3

y+

3

=0，得直线在x轴、y轴上的截距分别为-

3

，1．
∴B（0，1），F（-

3

，0），
则b=1，c=

3

，a=

b2+c2

=2，
∴椭圆的标准方程为

x2

4

+y2=1；                                       
（Ⅱ）由椭圆定义知|PF|=4-|PF′|，则|4-（|PF′|+|PB|）|=||PF|-|PB||，
而0≤||PF|-|PB||≤|BF|，
当且仅当|PF|=|PB|时，||PF|-|PB||=0，
当且仅当P是直线BF与椭圆C的交点时，||PF|-|PB||=|BF|=2，
∴|4-（|PF'|+|PB|）|的取值范围是[0，2]．                    
设P（m，n），由|PF|=|PB|，得

3

m+n+1=0，
由

m2 4 +n2=1 3 m+n+1=0

，
解得

m=0 n=-1

或

m=- 8 3 13 n= 11 13

，
∴使|4-（|PF′|+|PB|）|取得最小值时的P的坐标为（0，-1）和(-

8 3

13

，

11

13

)．

点评：本题是直线与圆锥曲线的综合问题，考查了椭圆方程的求法，考查了椭圆的定义，训练了数学转化思想方法，属中高档题．