题目内容
设集合A,B是非空集合M的两个不同子集,满足:A不是B的子集,且B也不是A的子集.
(1)若M={a1,a2,a3,a4},直接写出所有不同的有序集合对(A,B)的个数;
(2)若M={a1,a2,a3,…,an},求所有不同的有序集合对(A,B)的个数.
(1)若M={a1,a2,a3,a4},直接写出所有不同的有序集合对(A,B)的个数;
(2)若M={a1,a2,a3,…,an},求所有不同的有序集合对(A,B)的个数.
考点:排列、组合的实际应用,子集与真子集
专题:集合
分析:(1)根据定义,利用列举法即可得到结果;
(2)根据有序集合对的定义,利用数列的有关知识建立方程即可得到结论.
(2)根据有序集合对的定义,利用数列的有关知识建立方程即可得到结论.
解答:
解:(1)若集合A含有1个元素,则A有
=4,不妨设A={1},则B={2},{3},{4},{2,3},{2,4},{3,4},{2,3,4},此时B有7个,此时共有4×7=28个.
若集合A含有2个元素,则A有
=6种,不妨设A={1,2},则B={3},{4},{3,4},{1,4},{1,3},{1,3,4},{2,3},{2,4},{2,3,4},此时B有9个,此时共有6×9=54个.
若集合A含有3个元素,则A有
=4,不妨设A={1,2,3},则B={4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,3,4},此时B有7个,此时共有4×7=28个.
综上共有28+28+54=110种结果.
(2)集合M有2n个子集,不同的有序集合对(A,B)有2n(2n-1)个.
若A?B,并设B中含有k(1≤k≤n,k∈N•)个元素,则满足A?B的有序
集合对 (A,B) 有
(2k-1)=
•2k-
=3n-2n个.
同理,满足B?A的有序集合对(A,B)有3n-2n个.
故满足条件的有序集合对(A,B)的个数为2n(2n-1)-2(3n-2n)=4n+2n-2×3n.
| C | 1 4 |
若集合A含有2个元素,则A有
| C | 2 4 |
若集合A含有3个元素,则A有
| C | 3 4 |
综上共有28+28+54=110种结果.
(2)集合M有2n个子集,不同的有序集合对(A,B)有2n(2n-1)个.
若A?B,并设B中含有k(1≤k≤n,k∈N•)个元素,则满足A?B的有序
集合对 (A,B) 有
| n |
 |
| k=1 |
| C | k n |
| n |
 |
| k=0 |
| C | k n |
| n |
 |
| k=0 |
| C | k n |
同理,满足B?A的有序集合对(A,B)有3n-2n个.
故满足条件的有序集合对(A,B)的个数为2n(2n-1)-2(3n-2n)=4n+2n-2×3n.
点评:本题主要与集合有关是信息题,根据有序集合对的定义建立条件关系是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
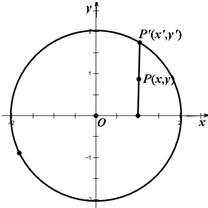 如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.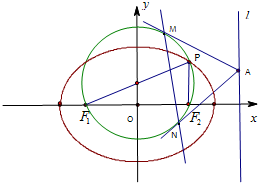 已知椭圆
已知椭圆