题目内容
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为
,且过点(4,-
).
(1)求此双曲线的方程;
(2)若点M(3,m)在双曲线上,求证:F1M⊥F2M.
| 2 |
| 10 |
(1)求此双曲线的方程;
(2)若点M(3,m)在双曲线上,求证:F1M⊥F2M.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由离心率为
,得c=
a,可得a=b,设双曲线方程为x2-y2=λ(λ≠0),将(4,-
)代入,求出λ,即可求双曲线的方程;
(2)将M(3,m)代入双曲线方程,得m=±
,证明kF1M•kF2M=-1,可得F1M⊥F2M.
| 2 |
| 2 |
| 10 |
(2)将M(3,m)代入双曲线方程,得m=±
| 3 |
解答:
(1)解:由离心率e=
=
,得c=
a,∴a=b,
设双曲线方程为x2-y2=λ(λ≠0),将(4,-
)代入得λ=6,
∴此双曲线的方程为x2-y2=6.
(2)证明:将M(3,m)代入双曲线方程,得m=±
,
∵F1(-2
,0),F2(2
,0),
∴kF1M•kF2M=
•
=-1,
∴F1M⊥F2M.
| c |
| a |
| 2 |
| 2 |
设双曲线方程为x2-y2=λ(λ≠0),将(4,-
| 10 |
∴此双曲线的方程为x2-y2=6.
(2)证明:将M(3,m)代入双曲线方程,得m=±
| 3 |
∵F1(-2
| 3 |
| 3 |
∴kF1M•kF2M=
| m | ||
3+2
|
| m | ||
3-2
|
∴F1M⊥F2M.
点评:本题考查双曲线的标准方程,考查点与双曲线的位置关系,考查学生的计算能力,正确求出双曲线的方程是关键.

练习册系列答案
相关题目
执行如图所示的程序框图,则输出S的值是( )


| A、10 | B、17 | C、26 | D、28 |
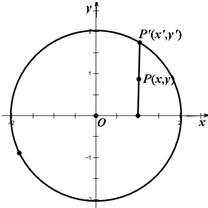 如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.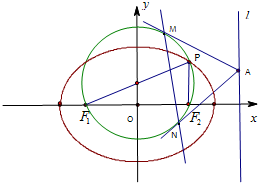 已知椭圆
已知椭圆