题目内容
已知点M是曲线C上任一点,点M到点F(1,0)的距离比到y轴的距离多1.
(1)求曲线C的方程;
(2)过点P(0,2)的直线L交曲线C于A、B两点,若以AB为直径的圆经过原点O,求直线L的方程.
(1)求曲线C的方程;
(2)过点P(0,2)的直线L交曲线C于A、B两点,若以AB为直径的圆经过原点O,求直线L的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出点M的轨迹是以F(1,0)为焦点,直线x=-1为准线的抛物线,由此能求出曲线C的方程.
(2)设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),由
,得ky2-4y+8=0,由此利用韦达定理和以AB为直径的圆过原点O求出k=-
,由此能求出直线l的方程.
(2)设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),由
|
| 1 |
| 2 |
解答:
解:(1)∵点M到点F(1,0)的距离比到y轴的距离多1,
∴点M到点F(1,0)的距离等于到直线x=-1的距离,
∴点M的轨迹是以F(1,0)为焦点,直线x=-1为准线的抛物线,
∴曲线C的方程为:y2=4x.
(2)设直线l的方程为y=kx+2(k≠0),
A(x1,y1),B(x2,y2),
由
,消去x得:ky2-4y+8=0,
则△=16-32k>0,解得k<
,
∴y1y2=
,x1x2=
•
=
,
∴以AB为直径的圆过原点O,
∴
•
=x1x2+y1y2=0,
∴
+
=0,解得k=-
,
∴直线l的方程为y=-
x+2.
∴点M到点F(1,0)的距离等于到直线x=-1的距离,
∴点M的轨迹是以F(1,0)为焦点,直线x=-1为准线的抛物线,
∴曲线C的方程为:y2=4x.
(2)设直线l的方程为y=kx+2(k≠0),
A(x1,y1),B(x2,y2),
由
|
则△=16-32k>0,解得k<
| 1 |
| 2 |
∴y1y2=
| 8 |
| k |
| y12 |
| 4 |
| y22 |
| 4 |
| 4 |
| k2 |
∴以AB为直径的圆过原点O,
∴
| OA |
| OB |
∴
| 4 |
| k2 |
| 8 |
| k |
| 1 |
| 2 |
∴直线l的方程为y=-
| 1 |
| 2 |
点评:本题考查曲线方程的求法,考查直线方程的求法,解题时要认真审题,注意根与系数关系的合理运用.

练习册系列答案
相关题目
执行如图所示的程序框图,则输出S的值是( )


| A、10 | B、17 | C、26 | D、28 |
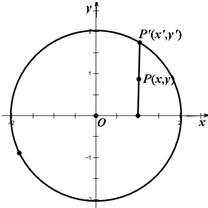 如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.