题目内容
若使得方程
-x-m=0有实数解,则实数m的取值范围为( )
| 16-x2 |
A、-4
| ||||
B、-4≤m≤4
| ||||
| C、-4≤m≤4 | ||||
D、4≤m≤4
|
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:将原式化为
=x+m,转化为y=
与y=x+m函数图象有公共点时,确定m的范围.
| 16-x2 |
| 16-x2 |
解答:
 解:
解:
-x-m=0可化为
=x+m,即问题转化为y=
与y=x+m有公共点
做出函数图象:
容易算出当直线y=x+m与半圆相切时m=4
,当直线过(4,0)点时m=-4.
故m的范围是-4≤m≤4
.
故选B.
 解:
解:| 16-x2 |
| 16-x2 |
| 16-x2 |
做出函数图象:
容易算出当直线y=x+m与半圆相切时m=4
| 2 |
故m的范围是-4≤m≤4
| 2 |
故选B.
点评:本题考查了利用函数的图象求解方程根的个数的问题,本题的关键:一是将根的个数问题转化为函数的零点问题,二是正确理解y=
的意义并画出图象.
| 16-x2 |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
已知实数x,y满足
,则x2+y2+4x+6y+14的最大值为( )
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
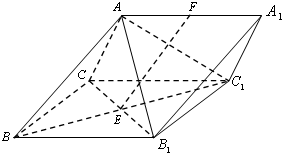 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,BC1与B1C的交点为E,AC=AB1,F为AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,BC1与B1C的交点为E,AC=AB1,F为AA1的中点.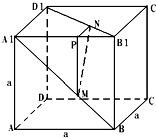 在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别为边A1B、B1D1、A1B1上的点,若
在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别为边A1B、B1D1、A1B1上的点,若