题目内容
已知直线a,b,c,d,给出以下四个命题:
①若a∥b,a⊥c,则b⊥c;
②若a⊥c,b⊥c,则a∥b;
③若a,b分别和异面直线c,d都相交,则a,b是异面直线;
④已知a,b是异面直线,若AB∥a,BC∥b,则∠ABC是异面直线a,b所成的角,
则以上命题中正确命题的序号是 .
①若a∥b,a⊥c,则b⊥c;
②若a⊥c,b⊥c,则a∥b;
③若a,b分别和异面直线c,d都相交,则a,b是异面直线;
④已知a,b是异面直线,若AB∥a,BC∥b,则∠ABC是异面直线a,b所成的角,
则以上命题中正确命题的序号是
考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离
分析:由垂直于两平行线中的一条,也垂直于另一条的性质,即可判断①;
空间中,垂直于同一直线的两直线平行、相交或异面,即可判断②;
比如空间四边形ABCD中,AD,BC为异面直线,AB,AC和它们都相交,但AB,AC相交,即可判断③;
已知a,b是异面直线,若AB∥a,BC∥b,则AB,AC所成的锐角或直角是异面直线a,b所成的角,即可判断④.
空间中,垂直于同一直线的两直线平行、相交或异面,即可判断②;
比如空间四边形ABCD中,AD,BC为异面直线,AB,AC和它们都相交,但AB,AC相交,即可判断③;
已知a,b是异面直线,若AB∥a,BC∥b,则AB,AC所成的锐角或直角是异面直线a,b所成的角,即可判断④.
解答:
解:对于①,若a∥b,a⊥c,由垂直于两平行线中的一条,也垂直于另一条的性质,可得b⊥c,故①对;
对于②,空间中,垂直于同一直线的两直线平行、相交或异面,故②错;
对于③,比如空间四边形ABCD中,AD,BC为异面直线,AB,AC和它们都相交,但AB,AC相交,故③错;
对于④,已知a,b是异面直线,若AB∥a,BC∥b,则AB,AC所成的锐角或直角是异面直线a,b所成的角,
故④错.
故答案为:①.
对于②,空间中,垂直于同一直线的两直线平行、相交或异面,故②错;
对于③,比如空间四边形ABCD中,AD,BC为异面直线,AB,AC和它们都相交,但AB,AC相交,故③错;
对于④,已知a,b是异面直线,若AB∥a,BC∥b,则AB,AC所成的锐角或直角是异面直线a,b所成的角,
故④错.
故答案为:①.
点评:本题考查空间两直线的位置关系:平行和相交或异面,考查异面直线所成的角的概念,是一道易错题,也是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
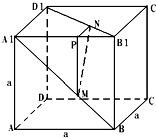 在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别为边A1B、B1D1、A1B1上的点,若
在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别为边A1B、B1D1、A1B1上的点,若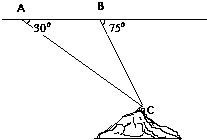 如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )
如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )