题目内容
在△ABC中，求证：
=
．
| a-ccosB |
| b-ccosA |
| sinB |
| sinA |
考点：余弦定理,正弦定理
专题：解三角形
分析：利用余弦定理化简等式的坐标为
，而由正弦定理可得
=
，从而证得要证的等式．
| b |
| a |
| b |
| a |
| sinB |
| sinA |
解答：
解：在△ABC中，由余弦定理可得
=
=
=
，而由正弦定理可得
=
，
∴
=
成立．
| a-ccosB |
| b-ccosA |
a-c•
| ||
b-c•
|
| b(a2+b2-c2) |
| a(a2+b2-c2) |
| b |
| a |
| b |
| a |
| sinB |
| sinA |
∴
| a-ccosB |
| b-ccosA |
| sinB |
| sinA |
点评：本题主要考查正弦定理和余弦定理的应用，属于基础题．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
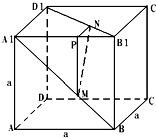在棱长为a的正方体ABCD-A1B1C1D1中，M、N、P分别为边A1B、B1D1、A1B1上的点，若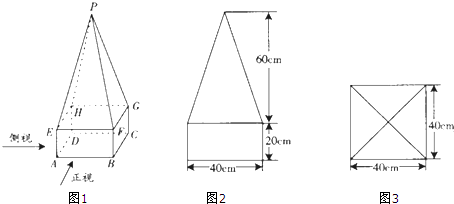
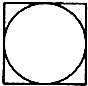如图是一个边长为1的正方形及其内切圆，现随机地向该正方形内投一粒黄豆（视为一点），则黄豆落入圆内的概率为