题目内容
已知椭圆C：
+
=1（a＞b＞0）经过点(
，1)，一个焦点是F（0，1）．
（1）求椭圆C的方程；
（2）若倾斜角为
的直线l与椭圆C交于A、B两点，且|AB|=
，求直线l的方程．
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 2 |
（1）求椭圆C的方程；
（2）若倾斜角为
| π |
| 4 |
12
| ||
| 7 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析：（1）首先利用椭圆经过的点求得方程
+
=1，利用焦点的坐标建立a2-b2=1解方程组得椭圆方程．
（2）根据直线的倾斜角为
，社直线的方程为y=x+b联立
+
=1以弦长公式为突破口，解方程求的结果．
| 1 |
| a2 |
| ||
| b2 |
（2）根据直线的倾斜角为
| π |
| 4 |
| 1 |
| a2 |
| ||
| b2 |
解答：
解：（1）椭圆C：
+
=1（a＞b＞0）经过点(
，1)，
则：
+
=1 ①
椭圆的一个焦点是F（0，1）．
则a2-b2=1 ②
由①②得：a2=4 b2=3
椭圆C的方程：
+
=1③
（2）根据题意可知：设直线l的方程为：y=x+b④
联立③④得：
3（x+b）2+4x2=12
整理得：7x2+6bx+3b2-12=0
∴x1+x2=-
x1x2=
∵|AB|=
=
|x1-x2|=
解方程得：b=±2
直线l的方程为：y=x±2
故答案为：（1）
+
=1
（2）直线l的方程为：y=x±2
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 2 |
则：
| 1 |
| a2 |
| ||
| b2 |
椭圆的一个焦点是F（0，1）．
则a2-b2=1 ②
由①②得：a2=4 b2=3
椭圆C的方程：
| y2 |
| 4 |
| x2 |
| 3 |
（2）根据题意可知：设直线l的方程为：y=x+b④
联立③④得：
|
3（x+b）2+4x2=12
整理得：7x2+6bx+3b2-12=0
∴x1+x2=-
| 6b |
| 7 |
| 3b2-12 |
| 7 |
∵|AB|=
12
| ||
| 7 |
| 2 |
| 2[(x1+x2)2-4x1x2] |
解方程得：b=±2
直线l的方程为：y=x±2
故答案为：（1）
| y2 |
| 4 |
| x2 |
| 3 |
（2）直线l的方程为：y=x±2
点评：本题考查的知识点：椭圆的方程的求法．直线方程的求法，弦长公式在直线与曲线相交中的应用，解一元二次方程及根和系数之间的关系．
练习册系列答案
相关题目
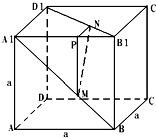在棱长为a的正方体ABCD-A1B1C1D1中，M、N、P分别为边A1B、B1D1、A1B1上的点，若