题目内容

若t2+4t＜mt，t∈[1，4]，求m的取值范围．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：构造函数f（t）=t2+4t-mt=t2+（4-m）t，由t∈[1，4]，t2+4t＜mt，可得：f（1）＜0，f（4）＜0，解不等式即可，
解答： 解：构造函数f（t）=t2+4t-mt=t2+（4-m）t，
由t∈[1，4]，t2+4t＜mt，
可得：f（1）＜0，f（4）＜0，
即
5-m＜0
16+4(4-m)＜0

解不等式组可得：m＞8
m的取值范围：m＞8
点评：本题考查了二次函数的性质，结合不等式求解．
练习册系列答案
相关题目
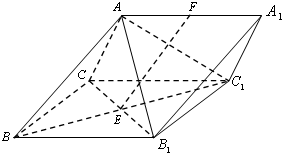如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，BC1与B1C的交点为E，AC=AB1，F为AA1的中点．
（1）求证：面FCB1⊥面ABC1；
（2）求证：EF∥面ABC．
奇函数f（x）的定义域为R，且在[0，+∞）上为增函数，问：是否存在m使f（x2-3）+f（2m-3x）＞f（0）对任意x∈[0，1]都成立？若存在，求出m的取值范围；若不存在，说明理由．
己知函数f（x）=
10x-99
x-10
，{an}为a1=1，d=2的等差数列，则f（a1）+f（a2）+f（a3）+…+f（a10）=
 
．
已知f（x）是定义在[-1，1]上的奇函数，且f（1）=2，任取a，b∈[-1，1]，a+b≠0，都有
f(a)+f(b)
a+b
＞0成立．
（1）证明函数f（x）在[-1，1]上是单调增函数．
（2）解不等式f（x）＜f（x2）．
（3）若对任意x∈[-1，1]，函数f（x）≤2m2-2am+3对所有的a∈[0，
3
2
]恒成立，求m的取值范围．
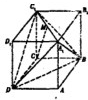如图，在长方体ABCD-A1B1C1D1中，AB=
2
，AD=AA1=1，M是A1C1的中点．
（1）求证：CM∥平面A1BD，
（2）求二面角A1-BD-C1的余弦值．
设偶函数y=f（x），对任意实数x∈R都有f（x）=f（x+4），当x∈[0，4]时，函数f（x）=ax2+x+b2-b-
11
4
（a∈R，b∈R），且当x∈[0，1]时，f（x）＜0恒成立，则b的取值范围是
 
．
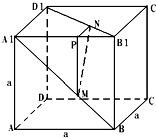在棱长为a的正方体ABCD-A1B1C1D1中，M、N、P分别为边A1B、B1D1、A1B1上的点，若
B1N
B1D1
=
BM
BA1
=
2
5
，求证：MN∥平面AA1D1D．
一般地，对于函数f（x）
 
，都有
 
，那么函数f（x）就叫做偶函数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网