题目内容
已知定义在R上的函数f(x)满足x>
时,f(x)>0,且f(
)=0,对任意m、n,f(m+n)=f(m)+f(n)+
,判断f(x)的单调性.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:抽象函数及其应用,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:由条件可令m=n=0,得到f(0),令m=x,n=-x,得到f(-x)=-f(x)-1.由于x>
时,f(x)>0,运用等式,推出x>0时,f(x)>-
,再由单调性的定义,即可得到函数f(x)的单调性.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由于任意m、n,f(m+n)=f(m)+f(n)+
,
令m=n=0,则f(0)=2f(0)+
,即有f(0)=-
,
令m=x,n=-x,则f(0)=f(x)+f(-x)+
,即有f(-x)=-f(x)-1.
由于x>
时,f(x)>0,
则f(x-
)=f(x)+f(-
)+
=f(x)-f(
)-
=f(x)-
>-
,
即有x>0时,f(x)>-
,
令x1<x2,则x2-x1>0,有f(x2-x1)=f(x2)+f(-x1)+
=f(x2)-f(x1)-1+
=f(x2)-f(x1)-
>-
,
即有f(x2)>f(x1),
故f(x)在R上为增函数.
| 1 |
| 2 |
令m=n=0,则f(0)=2f(0)+
| 1 |
| 2 |
| 1 |
| 2 |
令m=x,n=-x,则f(0)=f(x)+f(-x)+
| 1 |
| 2 |
由于x>
| 1 |
| 2 |
则f(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即有x>0时,f(x)>-
| 1 |
| 2 |
令x1<x2,则x2-x1>0,有f(x2-x1)=f(x2)+f(-x1)+
| 1 |
| 2 |
=f(x2)-f(x1)-1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即有f(x2)>f(x1),
故f(x)在R上为增函数.
点评:本题考查抽象函数及应用,考查函数的单调性的判断,注意运用定义,考查解决抽象函数的常用方法:赋值法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 若一个几何体的三视图,其正视图和侧视图均为矩形、俯视图为正三角形,尺寸如图所示,则该几何体的体积为( )
若一个几何体的三视图,其正视图和侧视图均为矩形、俯视图为正三角形,尺寸如图所示,则该几何体的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
若函数f(x)=ax2+bx+c满足f(4)=f(1),那么( )
| A、f(2)>f(3) |
| B、f(2)=f(3) |
| C、f(2)<f(3) |
| D、无法比较 |
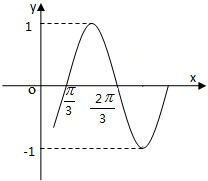 若函数y=Asin(ωx+φ)在平面直角坐标系中的图象(部分)如图所示,其中ω>0,|φ|≤π.
若函数y=Asin(ωx+φ)在平面直角坐标系中的图象(部分)如图所示,其中ω>0,|φ|≤π.