题目内容

若{an}为等差数列，Sn为其前n项和，若a1＞0，d＜0，S4=S10，则Sn＜0成立的最小的自然数n为
 
．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：运用等差数列的前n项和公式，结合函数求解．
解答： 解：∵{an}为等差数列，为其前n项和，
∴Sn=
d
2
n2+(a1-
d
2
)n，
根据二次函数的图象和性质
∵a1＞0，d＜0，S4=S10，
∴S7最大，S14=0，S15＜0
故答案为：15
点评：本题考察了等差数列的前n项和式子函数性．
练习册系列答案
相关题目
已知f（x）=xlnx．
（1）求函数y=f（x）的图象在x=e处的切线方程；
（2）设实数a＞0，求函数F（x）=
f(x)
a
在[a，2a]上的最大值．
若二次函数f（x）=x2-（a-1）x+5在区间（
1
2
，1）上是增函数，求a的取值范围．
若函数y=f（x）在区间（a，b）上是增函数，函数y=g（x）在区间（a，b）上是减函数，试判断函数y=f（x）-g（x）在区间（a，b）上的增减性；如果是y=f（x）+g（x）那么增减性又如何？
一个几何体的三视图如图所示，则此几何体的体积是（　　）
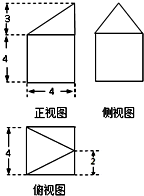
A、112B、80C、72D、64
已知定义在R上的函数f（x）满足x＞
1
2
时，f（x）＞0，且f（
1
2
）=0，对任意m、n，f（m+n）=f（m）+f（n）+
1
2
，判断f（x）的单调性．
已知函数y=4 x-
1
2
-3×2x+5（0≤x≤2），求函数的最值．
解不等式：2loga（x-4）＞loga（x-2）．
求函数y=丨x-1丨-丨x+2丨的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网