题目内容
已知数列{an}中满足a1=15,
=2,则
的最小值为( )
| an+1-an |
| n |
| an |
| n |
| A、10 | ||
B、2
| ||
| C、9 | ||
D、
|
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得an+1-an=2n,从而an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=n2-n+15,进而
=n+
-1,由此能求出当且仅当n=
,即n=4时,
取最小值4+
-1=
.
| an |
| n |
| 15 |
| n |
| 15 |
| n |
| an |
| n |
| 15 |
| 4 |
| 27 |
| 4 |
解答:
解:∵数列{an}中满足a1=15,
=2,
∴an+1-an=2n,
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=15+2+4+6+8+…+2(n-1)
=15+
×2
=n2-n+15,
∴
=n+
-1≥2
-1,
∴当且仅当n=
,即n=4时,
取最小值4+
-1=
.
故选:D.
| an+1-an |
| n |
∴an+1-an=2n,
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=15+2+4+6+8+…+2(n-1)
=15+
| (n-1)n |
| 2 |
=n2-n+15,
∴
| an |
| n |
| 15 |
| n |
| 15 |
∴当且仅当n=
| 15 |
| n |
| an |
| n |
| 15 |
| 4 |
| 27 |
| 4 |
故选:D.
点评:本题考查
的最小值的求法,是中档题,解题时要注意累加法和均值定理的合理运用.
| an |
| n |

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
函数y=x2-x,(-1<x<4)值域是( )
A、[-
| ||
| B、(2,12) | ||
| C、( 2,20) | ||
D、[-
|
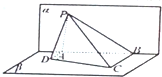 如图所示,△PAB所在的平面α和四边形AB所在的平面β互相垂直,AD⊥α,bc⊥α,AD=4,BC=8,AB=6,若tan∠ADP-2tan∠BCP=1,则动点P在平面内α的轨迹是( )
如图所示,△PAB所在的平面α和四边形AB所在的平面β互相垂直,AD⊥α,bc⊥α,AD=4,BC=8,AB=6,若tan∠ADP-2tan∠BCP=1,则动点P在平面内α的轨迹是( )| A、椭圆的一部分 |
| B、线段 |
| C、双曲线的一部分 |
| D、以上都不是 |
如果在约束条件
(0<a<1)下,目标函数x+ay最大值是
,则a=( )
|
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
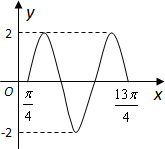 在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=