题目内容
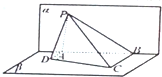如图所示，△PAB所在的平面α和四边形AB所在的平面β互相垂直，AD⊥α，bc⊥α，AD=4，BC=8，AB=6，若tan∠ADP-2tan∠BCP=1，则动点P在平面内α的轨迹是（ ）| A、椭圆的一部分 |
| B、线段 |
| C、双曲线的一部分 |
| D、以上都不是 |
考点：双曲线的定义,椭圆的定义
专题：计算题,圆锥曲线的定义、性质与方程
分析：由tan∠ADP=
，tan∠BCP=
，以及tan∠ADP-2tan∠BCP=1，可得|PA|-|PB|=4，根据双曲线的定义做出判断．
| |AP| |
| 4 |
| |PB| |
| 8 |
解答：
解：由题意得，△ADP 和△BCP均为直角三角形，且tan∠ADP=
，tan∠BCP=
．
∵tan∠ADP-2tan∠BCP=1，∴|PA|-|PB|=4＜|AB|=6，
故动点P在平面α内的轨迹是以A、B为焦点的双曲线的一支，
故选C．
| |AP| |
| 4 |
| |PB| |
| 8 |
∵tan∠ADP-2tan∠BCP=1，∴|PA|-|PB|=4＜|AB|=6，
故动点P在平面α内的轨迹是以A、B为焦点的双曲线的一支，
故选C．
点评：本题考查双曲线的定义，直角三角形中的边角关系，得到|PA|-|PB|=4＜|AB|是解题的关键．
练习册系列答案
相关题目
已知数列{an}中满足a1=15，
=2，则
的最小值为（ ）
| an+1-an |
| n |
| an |
| n |
| A、10 | ||
B、2
| ||
| C、9 | ||
D、
|
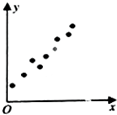已知变量x与y呈相关关系，且由观测数据得到的样本数据散点图如图所示，则由该观测数据算得的回归方程可能是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|