题目内容
已知函数f(x)=alnx-ax-3(a∈R).
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,问:m在什么范围取值时,函数g(x)=x3+x2[
+f′(x)],当且仅当在x=1处取得极值?
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,问:m在什么范围取值时,函数g(x)=x3+x2[
| m |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(I)求导数,利用导数的正负,可确定函数f(x)的单调区间;
(II)点(2,f(2))处的切线的倾斜角为45°,即切线斜率为1,即f'(2)=1,可求a值,代入得g(x)的解析式,求导函数,利用函数g(x)=x3+x2[
+f′(x)]在x=1时总存在极值,解方程,从而求出m的值.
(II)点(2,f(2))处的切线的倾斜角为45°,即切线斜率为1,即f'(2)=1,可求a值,代入得g(x)的解析式,求导函数,利用函数g(x)=x3+x2[
| m |
| 2 |
解答:
解:求导数可得:f'(x)=
-a(a>0)
(I)当a=1时,f′(x)=
,
令f'(x)>0时,解得0<x<1,所以f(x)的单调递增区间是(0,1);
令f'(x)<0时,解得x>1,所以f(x)的单调递减区间是(1,+∞).
(II)因为函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,所以f'(2)=1.
所以a=-2,∴f'(x)=
+2.
∴函数g(x)=x3+x2[
+2-
]=x3+(
+2)x2-2x,
∴g'(x)=3x2+(m+4)x-2
∵函数g(x)当且仅当在x=1处取得极值,g'(0)=-2<0
∴只需g ′(1)=3+m+4-2=0,
∴m=-5.
| a |
| x |
(I)当a=1时,f′(x)=
| 1-x |
| x |
令f'(x)>0时,解得0<x<1,所以f(x)的单调递增区间是(0,1);
令f'(x)<0时,解得x>1,所以f(x)的单调递减区间是(1,+∞).
(II)因为函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,所以f'(2)=1.
所以a=-2,∴f'(x)=
| -2 |
| x |
∴函数g(x)=x3+x2[
| m |
| 2 |
| 2 |
| x |
| m |
| 2 |
∴g'(x)=3x2+(m+4)x-2
∵函数g(x)当且仅当在x=1处取得极值,g'(0)=-2<0
∴只需g ′(1)=3+m+4-2=0,
∴m=-5.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的极值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知等差数列{an}中,a6+a8=10,a3=1,则a11的值是( )
| A、15 | B、9 | C、10 | D、11 |
执行图示的程序框图,如果输入的x∈[-2,2],则输出的y属于( )

A、[
| ||
B、(
| ||
C、[
| ||
D、(
|
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.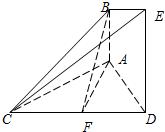 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点. 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.