题目内容

甲乙两台机床同时生产一种零件，10天中，两台机床每天出的次品数分别是：
甲 4  1  0  2  2  1  3  1  2  4
乙 2  3  1  1  3  2  2  1  2  3
计算上述两组数据的平均数和方差，从统计结果看，那台机床的性能较好？
考点：极差、方差与标准差,众数、中位数、平均数
专题：概率与统计
分析：分别求出两台机床的平均数和方差，由
.
x甲
=
.
x乙
，S甲2＞S乙2，得到乙台机床的性能较好．
解答： 解：
.
x甲
=
1
10
（4+1+0+2+2+1+3+1+2+4）=2，
.
x乙
=
1
10
（2+3+1+1+3+2+2+1+2+3）=2，
S甲2=
1
10
[（4-2）2+（1-2）2+（0-2）2+（2-2）2+（2-2）2+
（1-2）2+（3-2）2+（1-2）2+（2-2）2+（4-2）2=1.6．
S乙2=
1
10
[（2-2）2+（3-2）2+（1-2）2+（1-2）2+（3-2）2+
（2-2）2+（2-2）2+（1-2）2+（2-2）2+（3-2）2=0.6．
∵
.
x甲
=
.
x乙
，S甲2＞S乙2，
∴乙台机床的性能较好．
点评：本题考查平均数和方差的计算，是基础题，解题时要注意方差公式的合理运用．
练习册系列答案
相关题目
直线2ay-x=0与直线（3a-1）x-ay-1=0平行且不重合，则a等于（　　）
A、
1
2
B、
1
6
C、0或
1
2
D、0或
1
6
直线l1：（
2
-1）x+y-2=0与直线l2：（
2
+1）x-y-3=0的位置关系是（　　）
A、平行B、相交C、垂直D、重合
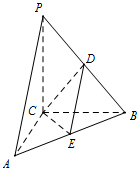如图，在三棱锥P-ABC中，PB⊥AC，PC⊥平面ABC，点D，E分别为线段PB，AB的中点．
（1）求证：AC⊥平面PBC；
（2）设二面角D-CE-B的平面角为θ，若PC=BC=2，AC=2
3
，求cosθ的值．
已知函数f（x）=alnx-ax-3（a∈R）．
（Ⅰ）当a=1时，求函数f（x）的单调区间；
（Ⅱ）若函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，问：m在什么范围取值时，函数g（x）=x3+x2[
m
2
+f′（x）]，当且仅当在x=1处取得极值？
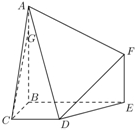如图，多面体ABCDEF中，BA、BC、BE两两垂直，且AB∥EF，CD∥BE，AB=BE=2，BC=CD=EF=1．
（Ⅰ）若点G在线段AB上，且BG=3GA，求证：CG∥平面ADF；
（Ⅱ）求证：平面ABD⊥平面DEF．
（Ⅲ）求直线DF与平面ABEF所成的角的正弦值．
若函数y=
f(x)
x
在（m，+∞）上为增函数（m为常数），则称f（x）为区间（m，+∞）上的“一阶比增函数”．
已知函数f（x）是在（0，+∞）上每一点处可导的函数，且xf′（x）＞f（x）在（0，+∞）上恒成立．
（1）求证：f（x）为区间（0，+∞）上的“一阶比增函数”；
（2）当x1＞0，x2＞0时，证明：f（x1）+f（x2）＜f（x1+x2）；
（3）已知不等式ln（l+x）＜x在x＞-1且x≠0时恒成立，证明：
1
22
ln2+
1
33
ln4+…+
1
(n+1)2
ln（n+1）＞
n
4(n+1)(n+2)
（n∈N*）．
设数列{an}的各项均为正数，它的前n项的和为Sn，点（an，Sn）在函数y=
1
8
x2+
1
2
x+
1
2
的图象上；数列{bn}满足b1=a1，bn+1（an+1-an）=bn．其中n∈N*．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）设cn=
an
bn
，求证：数列{cn}的前n项的和Tn＞
5
9
（n∈N*）．
某企业主要生产甲、乙两种品牌的空调，由于受到空调在保修期内维修费等因素的影响，企业生产每台空调的利润与该空调首次出现故障的时间有关，甲、乙两种品牌空调的保修期均为3年，现从该厂已售出的两种品牌空调中各随机抽取50台，统计数据如下：
品牌甲乙
首次出现故障时间
x年		0＜x≤11＜x≤22＜x≤3x＞30＜x≤22＜x≤3x＞3
空调数量（台）124432345
每台利润（千元）122.52.71.52.62.8
将频率视为概率，解答下列问题：
（Ⅰ）从该厂生产的甲品牌空调中随机抽取一台，求首次出现故障发生在保修期内的概率；
（Ⅱ）若该厂生产的空调均能售出，记生产一台甲品牌空调的利润为X1，生产一台乙品牌空调的利润为X2，分别求X1，X2的分布列；
（Ⅲ）该厂预计今后这两种品牌空调销量相当，但由于资金限制，只能生产其中一种品牌空调，若从经济效益的角度考虑，你认为应该生产哪种品牌的空调？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网