题目内容
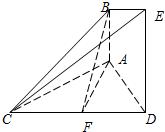 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.(1)求三棱锥D-BAC的体积;
(2)求证:AF∥平面BCE;
(3)求二面角B-CD-A的大小.
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件得S△ACD=
×4=
,由线面垂直得BA是三棱锥B-ACD的高,且BA=1,由此能求出三棱锥D-BAC的体积.
(2)取CE的中点为H,连接BH,FH,由已知条件推导出四边形BHFA是平行四边形,由此能证明AF∥平面BCE.
(3)连接BD,由已知条件推导出∠BFA就是二面角B-CD-A的平面角,由此能求出二面角B-CD-A的大小.
| ||
| 4 |
| 3 |
(2)取CE的中点为H,连接BH,FH,由已知条件推导出四边形BHFA是平行四边形,由此能证明AF∥平面BCE.
(3)连接BD,由已知条件推导出∠BFA就是二面角B-CD-A的平面角,由此能求出二面角B-CD-A的大小.
解答:
(本小题满分14分)
(1)解:∵△ACD为等边三角形,且边长为2,
∴S△ACD=
×4=
…(1分)
∵AB⊥平面ACD,∴BA是三棱锥B-ACD的高,且BA=1,
∴VB-ACD=
×
×1=
,…(3分)
∴VD-ACB=VB-ACD=
.
∴三棱锥D-BAC的体积为
.…(4分)
(2)证明:取CE的中点为H,连接BH,FH,
∵F为CD的中点,∴FH∥ED且FH=
ED…(5分)
∵AB⊥平面ACD,DE⊥平面ACD,AB=
ED,
∴FH∥AB,且FH=AB…(6分)
∴四边形BHFA是平行四边形,即BH∥FA…(7分)
∵BH?平面BCE,FA?平面BCE,
∴AF∥平面BCE.…(8分)
(3)连接BD,在等边三角形△ACD中,F为CD的中点,∴AF⊥CD,…(9分)
∵AB⊥平面ACD,∴∠BAD=90°∵AD=2,BA=1,
由勾股定理得BD=
.
同理可得BC=
,∴BC=BD,∵F为CD的中点,∴BF⊥CD…(11分)
∴∠BFA就是二面角B-CD-A的平面角…(12分)
则tan∠BFA=
=
=
,…(13分)
∴二面角B-CD-A的大小为
.…(14分)
(1)解:∵△ACD为等边三角形,且边长为2,
∴S△ACD=
| ||
| 4 |
| 3 |
∵AB⊥平面ACD,∴BA是三棱锥B-ACD的高,且BA=1,
∴VB-ACD=
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
∴VD-ACB=VB-ACD=
| 1 |
| 3 |
| 3 |
∴三棱锥D-BAC的体积为
| 1 |
| 3 |
| 3 |
(2)证明:取CE的中点为H,连接BH,FH,
∵F为CD的中点,∴FH∥ED且FH=
| 1 |
| 2 |
∵AB⊥平面ACD,DE⊥平面ACD,AB=
| 1 |
| 2 |
∴FH∥AB,且FH=AB…(6分)
∴四边形BHFA是平行四边形,即BH∥FA…(7分)
∵BH?平面BCE,FA?平面BCE,
∴AF∥平面BCE.…(8分)
(3)连接BD,在等边三角形△ACD中,F为CD的中点,∴AF⊥CD,…(9分)
∵AB⊥平面ACD,∴∠BAD=90°∵AD=2,BA=1,
由勾股定理得BD=
| 5 |
同理可得BC=
| 5 |
∴∠BFA就是二面角B-CD-A的平面角…(12分)
则tan∠BFA=
| BA |
| AF |
| 1 | ||
|
| ||
| 3 |
∴二面角B-CD-A的大小为
| π |
| 6 |
点评:本题考查三棱锥体积的求法,考查直线与平面平行的证明,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
正三棱锥的高和底面边长都等于6,则其外接球的表面积为( )
| A、8π | B、16π |
| C、32π | D、64π |
从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有( )
| A、180种 | B、280种 |
| C、96种 | D、240种 |
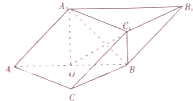 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.