题目内容
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.(Ⅰ)求证:平面ADF⊥平面CBF;
(Ⅱ)求证:PM∥平面AFC;
(Ⅲ)求多面体CD-AFEB的体积V.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出CB⊥平面ABEF,CB⊥AF,AF⊥BF,由此能证明平面ADF⊥平面CBF.
(Ⅱ)连结OM延长交BF于H,由已知条件得PH∥CF,从而得到PH∥平面AFC,连结PO,由已知条件推导出PO∥平面AFC,所以平面POO1∥平面AFC,由此能证明PM∥平面AFC.
(Ⅲ)多面体CD-AFEB的体积可分成三棱锥C-BEF与四棱锥F-ABCD的体积之和,由此能求出结果.
(Ⅱ)连结OM延长交BF于H,由已知条件得PH∥CF,从而得到PH∥平面AFC,连结PO,由已知条件推导出PO∥平面AFC,所以平面POO1∥平面AFC,由此能证明PM∥平面AFC.
(Ⅲ)多面体CD-AFEB的体积可分成三棱锥C-BEF与四棱锥F-ABCD的体积之和,由此能求出结果.
解答:
(本小题满分12分)
(Ⅰ)证明:∵矩形ABCD所在的平面和平面ABEF互相垂直,且CB⊥AB.
∴CB⊥平面ABEF,
又AF?平面ABEF,所以CB⊥AF,(1分)
又AB=2,AF=1,∠BAF=60°,
由余弦定理知BF=
,
∴AF2+BF2=AB2,得AF⊥BF,(2分)
AF∩CB=B∴AF⊥平面CFB,(3分)
∵AF?平面AFC,∴平面ADF⊥平面CBF.(4分)
(Ⅱ)证明:连结OM延长交BF于H,
则H为BF的中点,又P为CB的中点,
∴PH∥CF,又∵AF?平面AFC,∴PH∥平面AFC,(5分)
连结PO,则PO∥AC,AC?平面AFC,PO∥平面AFC,(6分)
∵PO∩PO1=P,∴平面POO1∥平面AFC,(7分)
PM?平面AFC,PM∥平面AFC.(8分)
(Ⅲ)解:多面体CD-AFEB的体积可分成三棱锥C-BEF与
四棱锥F-ABCD的体积之和,(9分)
在等腰梯形ABCF中,计算得EF=1,两底间的距离EE1=
∴VC-BEF=
S△BEF×CB=
×
×1×
×1=
,(10分)
VF-ABCD=
SEFCD×EE1=
×2×1×
=
,(11分)
∴V=VC-BEF+VF-ABCD=
.(12分)
(Ⅰ)证明:∵矩形ABCD所在的平面和平面ABEF互相垂直,且CB⊥AB.
∴CB⊥平面ABEF,
又AF?平面ABEF,所以CB⊥AF,(1分)
又AB=2,AF=1,∠BAF=60°,
由余弦定理知BF=
| 3 |
∴AF2+BF2=AB2,得AF⊥BF,(2分)
AF∩CB=B∴AF⊥平面CFB,(3分)
∵AF?平面AFC,∴平面ADF⊥平面CBF.(4分)
(Ⅱ)证明:连结OM延长交BF于H,
则H为BF的中点,又P为CB的中点,
∴PH∥CF,又∵AF?平面AFC,∴PH∥平面AFC,(5分)
连结PO,则PO∥AC,AC?平面AFC,PO∥平面AFC,(6分)
∵PO∩PO1=P,∴平面POO1∥平面AFC,(7分)
PM?平面AFC,PM∥平面AFC.(8分)
(Ⅲ)解:多面体CD-AFEB的体积可分成三棱锥C-BEF与
四棱锥F-ABCD的体积之和,(9分)
在等腰梯形ABCF中,计算得EF=1,两底间的距离EE1=
| ||
| 2 |
∴VC-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
VF-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴V=VC-BEF+VF-ABCD=
5
| ||
| 12 |
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查多面体和体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
抛物线x2=(2a-1)y的准线方程为y=1,则实数a=( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若圆的方程为
(θ为参数),当θ=
时,对应点的坐标是( )
|
| π |
| 2 |
| A、(2,0) |
| B、(0,2) |
| C、(-2,0) |
| D、(0,-2) |
直线l1:(
-1)x+y-2=0与直线l2:(
+1)x-y-3=0的位置关系是( )
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |
从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有( )
| A、180种 | B、280种 |
| C、96种 | D、240种 |
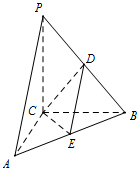 如图,在三棱锥P-ABC中,PB⊥AC,PC⊥平面ABC,点D,E分别为线段PB,AB的中点.
如图,在三棱锥P-ABC中,PB⊥AC,PC⊥平面ABC,点D,E分别为线段PB,AB的中点.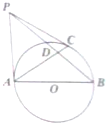 如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.
如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.