题目内容
 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.(Ⅰ)求直线EC与平面ABE所成角的正切值;
(Ⅱ)线段EA上是否存在点F,使EC∥平面FBD?存在请确定具体位置,不存在说明理由.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)根据线面所成角的定义,即可求直线EC与平面ABE所成角的正切值;
(Ⅱ)建立空间直角坐标系,利用向量法结合EC∥平面FBD,即可得到结论.
(Ⅱ)建立空间直角坐标系,利用向量法结合EC∥平面FBD,即可得到结论.
解答:
解:(Ⅰ)∵平面ABCD⊥平面ABE,且交线AB,BC⊥AB,BC?平面ABCD,
∴BC⊥平面ABE,
则∠CEB是直线EC与平面ABE所成角,
∵在等腰三角形ABE中,AB=2,
∴EB=EA=
,
在直角三角形CBE中,tan∠CEB=
=
=
,
∴直线EC与平面ABE所成角的正切值为
.
(Ⅱ)设O为AB的中点,连接OD,OE,则OE⊥AB,
∵平面ABCD⊥平面ABE,
∴OE⊥平面ABE,OE⊥OD,
在直角梯形ABCD,由CD=OB,CD∥OB,可得OD⊥AB,
由OB,OD,OE两两垂直,建立空间直角坐标系O-xyz,
假设线段EA上存在点F,使EC∥平面FBD,
设
=(x,y,z)是平面PBD的一个法向量,则必需使
⊥
.
∵E(0,0,1),C(1,-1,0),B(0,-1,0),D(1,0,0)
则
=(1,-1,-1),
=(1,1,0),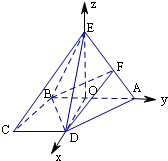
设F(0,a,1-a)
=(-1,a,1-a),
∴
,得
令x=1,则
=(1,-1,
).
要使
⊥
,则有1+1+
=0,∴a=
.
此时F(0,
,
),
=(0,
,-
),
=(0,1,-1),
∴
=
则线段EA上存在点F,且是靠近点E的一个三等分点.
∴BC⊥平面ABE,
则∠CEB是直线EC与平面ABE所成角,
∵在等腰三角形ABE中,AB=2,
∴EB=EA=
| 2 |
在直角三角形CBE中,tan∠CEB=
| BC |
| BE |
| 1 | ||
|
| ||
| 2 |
∴直线EC与平面ABE所成角的正切值为
| ||
| 2 |
(Ⅱ)设O为AB的中点,连接OD,OE,则OE⊥AB,
∵平面ABCD⊥平面ABE,
∴OE⊥平面ABE,OE⊥OD,
在直角梯形ABCD,由CD=OB,CD∥OB,可得OD⊥AB,
由OB,OD,OE两两垂直,建立空间直角坐标系O-xyz,
假设线段EA上存在点F,使EC∥平面FBD,
设
| n |
| EC |
| n |
∵E(0,0,1),C(1,-1,0),B(0,-1,0),D(1,0,0)
则
| EC |
| BD |

设F(0,a,1-a)
| DF |
∴
|
|
令x=1,则
| n |
| 1+a |
| 1-a |
要使
| EC |
| n |
| 1+a |
| 1-a |
| 1 |
| 3 |
此时F(0,
| 1 |
| 3 |
| 2 |
| 3 |
| EF |
| 1 |
| 3 |
| 1 |
| 3 |
| EA |
∴
| EF |
| 1 |
| 3 |
| EA |
则线段EA上存在点F,且是靠近点E的一个三等分点.
点评:本题主要考查直线和平面所成角的计算,以及线面平行的判断,建立空间坐标系是解决本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
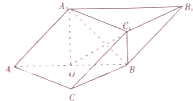 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.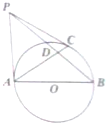 如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.
如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D. 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,