题目内容
设F1,F2是椭圆的两个焦点,点P是以线段F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则此椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知可得∠F1PF2=90°,再由∠PF1F2=5∠PF2F1求出∠PF1F2=15°,∠PF2F1=75°,结合正弦定理得到a,c的关系,则答案可求.
解答:
解:∵P是以F1F2为直径的圆与椭圆的一个交点,
∴∠F1PF2=90°,
∵∠PF1F2=5∠PF2F1,
∴∠PF1F2=15°,∠PF2F1=75°,
∴|PF1|=|F1F2|sin∠PF2F1=2c•sin75°,
∴|PF2|=|F1F2|sin∠PF1F2=2c•sin15°,
∴2a=|PF1|+|PF2|=2c•sin75°+2c•sin15°=4csin45°cos30°=4×
×
c=
c,
∴a=
c,
∴e=
=
.
故选:B.
∴∠F1PF2=90°,
∵∠PF1F2=5∠PF2F1,
∴∠PF1F2=15°,∠PF2F1=75°,
∴|PF1|=|F1F2|sin∠PF2F1=2c•sin75°,
∴|PF2|=|F1F2|sin∠PF1F2=2c•sin15°,
∴2a=|PF1|+|PF2|=2c•sin75°+2c•sin15°=4csin45°cos30°=4×
| ||
| 2 |
| ||
| 2 |
| 6 |
∴a=
| ||
| 2 |
∴e=
| c |
| a |
| ||
| 3 |
故选:B.
点评:本题考查了椭圆的简单几何性质,考查了椭圆定义的运用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=min{3+log
x,log2x},其中min{p,q}表示p,q两者中的较小者,则f(x)<2的解集为( )
| 1 |
| 4 |
| A、0<x<4或x>4 |
| B、0<x<4 |
| C、x>4 |
| D、0<x<3或x>3 |
已知平面向量
,
(
≠0,
≠
)满足|
|=1,且
与
-
的夹角为30°,则|
|的取值范围是( )
| α |
| β |
| α |
| α |
| β |
| β |
| α |
| α |
| β |
| α |
A、(0,
| ||||
| B、(0,2] | ||||
C、(1,
| ||||
| D、(1,2] |
已知球的半径为R,则半球的最大内接正方体的边长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、(
|
函数f(x)=lnx-1的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
过正三棱锥一侧棱及其外接球的球心O所作截面如图所示,则这个正三棱锥的侧面三角形的顶角为( )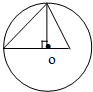

| A、60° | ||
| B、90° | ||
| C、120° | ||
D、arccos
|