题目内容
已知△ABC中
=(k,1),
=(2,4),|
|≤
.
(Ⅰ)若k∈Z,求△ABC是直角三角形的概率;
(Ⅱ)若k∈R,求△ABC中B是钝角的概率.
| AB |
| AC |
| AB |
| 10 |
(Ⅰ)若k∈Z,求△ABC是直角三角形的概率;
(Ⅱ)若k∈R,求△ABC中B是钝角的概率.
考点:几何概型,古典概型及其概率计算公式
专题:
分析:利用向量的模求出k的范围,
(Ⅰ)k∈Z,求出直角三角形的个数与所有基本事件的个数,即可利用古典概型求△ABC是直角三角形的概率;
(Ⅱ)k∈R,求出求解长度,利用几何概型求△ABC中B是钝角的概率.
(Ⅰ)k∈Z,求出直角三角形的个数与所有基本事件的个数,即可利用古典概型求△ABC是直角三角形的概率;
(Ⅱ)k∈R,求出求解长度,利用几何概型求△ABC中B是钝角的概率.
解答:
解:由已知
=(k,1),
=(2,4),|
|≤
,得-3≤k≤3,
=(2-k,3)
(I)若k∈Z,Ω={-3,-2,-1,0,1,2,3},k的总数n=7.
若A是直角,则k=-2;
若B是直角,则k(2-k)+3=0,k=-1,k=3;
若C是直角,则2(2-k)+12=0,k=8;
故符合条件k的个数m=3,△ABC是直角三角形的概率为P=
=
. (4分)
(II)若k∈R,-3≤k≤3,且k≠
,区间长度L=6.
若B是钝角,则k(2-k)+3<0,-1<k<3,区间长度L′=4.
△ABC中B是钝角的概率P=
=
. (6分)
| AB |
| AC |
| AB |
| 10 |
| BC |
(I)若k∈Z,Ω={-3,-2,-1,0,1,2,3},k的总数n=7.
若A是直角,则k=-2;
若B是直角,则k(2-k)+3=0,k=-1,k=3;
若C是直角,则2(2-k)+12=0,k=8;
故符合条件k的个数m=3,△ABC是直角三角形的概率为P=
| m |
| n |
| 3 |
| 7 |
(II)若k∈R,-3≤k≤3,且k≠
| 1 |
| 2 |
若B是钝角,则k(2-k)+3<0,-1<k<3,区间长度L′=4.
△ABC中B是钝角的概率P=
| L′ |
| L |
| 2 |
| 3 |
点评:本题考查几何概型以及古典概型的概率的求法,基本知识的考查.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
设F1,F2是椭圆的两个焦点,点P是以线段F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则此椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f(x)、g(x)的定义域分别为F、G,且F⊆G.若对任意的x∈F,都有f(x)=g(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知f(x)=2x(x≤0),若g(x)为f(x)在R上的一个延拓函数,且g(x)是偶函数,则g(x)的解析式是( )
| A、log2|x| | ||
| B、2|x| | ||
C、log
| ||
D、(
|
执行如图的程序,则输出的结果等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
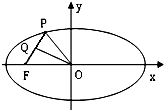 如图,P是椭圆
如图,P是椭圆