题目内容
已知平面向量
,
(
≠0,
≠
)满足|
|=1,且
与
-
的夹角为30°,则|
|的取值范围是( )
| α |
| β |
| α |
| α |
| β |
| β |
| α |
| α |
| β |
| α |
A、(0,
| ||||
| B、(0,2] | ||||
C、(1,
| ||||
| D、(1,2] |
考点:平面向量数量积的运算
专题:计算题,三角函数的图像与性质,平面向量及应用
分析:设
=
,
=
,则
=
-
,由已知
与
-
的夹角为30°可得∠ABC=30°,运用正弦定理结合正弦函数的值域,从而可求|
|的取值范围.
| AB |
| α |
| AC |
| β |
| CB |
| α |
| β |
| α |
| α |
| β |
| α |
解答:
解:设
=
,
=
,则由
=
-
,
又∵
与
-
的夹角为30°
∴∠ABC=30°
又由|
|=|
|=1,
由正弦定理
=
得:
|
|=2sinC≤2.
∴|
|∈(0,2]
故选B.
| AB |
| α |
| AC |
| β |
| CB |
| α |
| β |
又∵
| α |
| α |
| β |
∴∠ABC=30°
又由|
| AC |
| β |
由正弦定理
|
| ||
| sinC |
|
| ||
| sin30° |
|
| α |
∴|
| α |
故选B.
点评:本题主考查了向量的加法运算的三角形法则,考查了三角形的正弦定理及三角函数的性质,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
设F1,F2是椭圆的两个焦点,点P是以线段F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则此椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图的程序,则输出的结果等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
甲,乙两位同学考入某大学的同一专业,已知该专业设有3个班级,则他们被随机分到同一个班级的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
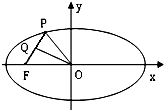 如图,P是椭圆
如图,P是椭圆