题目内容
过正三棱锥一侧棱及其外接球的球心O所作截面如图所示,则这个正三棱锥的侧面三角形的顶角为( )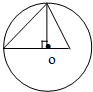

| A、60° | ||
| B、90° | ||
| C、120° | ||
D、arccos
|
考点:球内接多面体
专题:计算题,空间位置关系与距离
分析:底面正三角形在球的大圆上,且圆心是正三角形的中心,从而求出底、高、侧棱长,利用余弦定理,即可得出结论.
解答:
解:设半径为R,由图可知,底面正三角形在球的大圆上,
则正三角形的高为
,边长为
R.正三棱锥的高为R.
则侧面三角形的底边长为
R,高为
=
R,侧棱长为
R;
设正三棱锥的侧面三角形的顶角为α,则cosα=
=
,
∴正三棱锥的侧面三角形的顶角为arccos
,
故选:D.
则正三角形的高为
| 3R |
| 2 |
| 3 |
则侧面三角形的底边长为
| 3 |
R2+(
|
| ||
| 2 |
| 2 |
设正三棱锥的侧面三角形的顶角为α,则cosα=
| 2R2+2R2-3R2 | ||||
2×
|
| 1 |
| 4 |
∴正三棱锥的侧面三角形的顶角为arccos
| 1 |
| 4 |
故选:D.
点评:考查了学生的空间想象力,及组合体中角的求法,比较基础.

练习册系列答案
相关题目
设F1,F2是椭圆的两个焦点,点P是以线段F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则此椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
甲,乙两位同学考入某大学的同一专业,已知该专业设有3个班级,则他们被随机分到同一个班级的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={1,2},B={2,3,4},则A∩B=( )
| A、{1,2,3,4} |
| B、{1,2,2,3,4} |
| C、{2} |
| D、{1,3,4} |