题目内容
若函数f(x)为偶函数,x>0时,f(x)递增,P=f(-π),Q=f(e),R=f(lnπ),则( )
| A、P>Q>R |
| B、R>Q>P |
| C、P>R>Q |
| D、Q>R>P |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由函数f(x)为偶函数,可得P=f(-π)=f(π),进而上x>0时,f(x)递增,比较三个自变量的大小,可得结论.
解答:
解:∵函数f(x)为偶函数,
∴P=f(-π)=f(π),
∵x>0时,f(x)递增,且π>e>lnπ>0,
故P>Q>R,
故选:A
∴P=f(-π)=f(π),
∵x>0时,f(x)递增,且π>e>lnπ>0,
故P>Q>R,
故选:A
点评:本题考查的知识点是函数奇偶性的性质,其中熟练掌握偶函数满足f(-x)=f(x),是解答的关键.

练习册系列答案
相关题目
集合A={x|2x-x2>0},B={x|1≤x<2},则∁AB=( )
| A、(0,1) |
| B、(0,1] |
| C、[0,1] |
| D、(1,2) |
设变量x,y满足
,若目标函数z=x-y+1的最小值为0,则m的值为( )
|
| A、4 | B、5 | C、6 | D、7 |
已知i为虚数单位,复数z=-
+
i的共轭复数为
,则
+|z|( )
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
. |
| z |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
已知向量
=(1,2),
=(2,-1),下列结论中不正确的是( )
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、
|
在△ABC中,∠A<30°是cosA>
的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
一个空间几何体的三视图如图所示,则该几何体的体积为( )
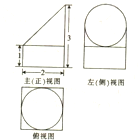

A、4+
| ||
| B、4+π | ||
| C、4+2π | ||
| D、以上都不对 |
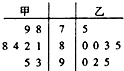 甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示.
甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示.