题目内容
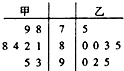 甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示.
甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示.(1)指出学生乙成绩的中位数,并说明如何确定一组数据的中位数;
(2)现要从中选派一人参加数学竞赛,你认为派哪位学生参加,成绩比较稳定?
(3)若将频率视为概率,请预测学生甲在今后一次数学竞赛中成绩高于80分的概率.
考点:古典概型及其概率计算公式,茎叶图,众数、中位数、平均数
专题:概率与统计
分析:(1)根据中位数的定义进行确定.
(2)利用平均数和方差的定义进行求值判断.
(2)利用平均数和方差的定义进行求值判断.
解答:
解:(1)乙中共有8个数据,则位于中间的两个数为83,85,∴中位数为
(83+85)=84.
(2)甲的平均数为
甲=
(78+79+81+82+84+88+93+95)=85,
乙的平均数为
=
(75+80+80+83+85+90+95)=85,
∴
=
.
方差
=
[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(93-85)2+(95-85)2]=35.5,
方差
=
[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(90-85)2+(92-85)2+(95-85)2]═41,
∵
,∴甲成绩稳定.
故应派甲去参加比赛.
(3)由题意得P=
=
.
| 1 |
| 2 |
(2)甲的平均数为
. |
| x |
| 1 |
| 8 |
乙的平均数为
. |
| x乙 |
| 1 |
| 8 |
∴
. |
| x甲 |
. |
| x乙 |
方差
| S | 2 甲 |
| 1 |
| 8 |
方差
| S | 2 乙 |
| 1 |
| 8 |
∵
| S | 2 甲 |
| <S | 2 乙 |
故应派甲去参加比赛.
(3)由题意得P=
| 6 |
| 8 |
| 3 |
| 4 |
点评:本题主要考查统计的有关知识,要求熟练掌握中位数,平均数和方差的公式.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
若函数f(x)为偶函数,x>0时,f(x)递增,P=f(-π),Q=f(e),R=f(lnπ),则( )
| A、P>Q>R |
| B、R>Q>P |
| C、P>R>Q |
| D、Q>R>P |
设
,
为两个非零向量,则“
•
=|
•
|”是“
与
共线”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
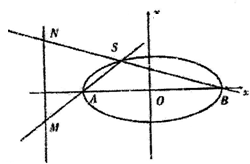 如图,已知椭圆C:
如图,已知椭圆C: 已知椭圆C:
已知椭圆C: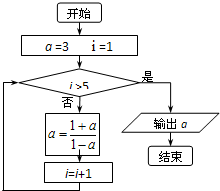
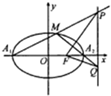 如图,A1(-2,0),A2(2,0)是椭圆C:
如图,A1(-2,0),A2(2,0)是椭圆C: