题目内容
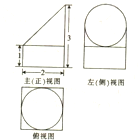
一个空间几何体的三视图如图所示，则该几何体的体积为（ ）
A、4+
| ||
| B、4+π | ||
| C、4+2π | ||
| D、以上都不对 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可知，该几何体是一个被斜截的圆柱和一个长方体的组合体，分别求出两个简单几何体的体积，相加可得答案．
解答：
解：由已知中的三视图可知，该几何体是一个被斜截的圆柱和一个长方体的组合体，
其中上部分相当于一个底面直径为2，高为3的圆柱体积的一半，
故其体积为：
×π×(
)2×3=
π，
下部长方体的长宽高分别为2，2，1，故体积为：2×2×1=4，
故组合体的体积为4+
π，
故选：D
其中上部分相当于一个底面直径为2，高为3的圆柱体积的一半，
故其体积为：
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
下部长方体的长宽高分别为2，2，1，故体积为：2×2×1=4，
故组合体的体积为4+
| 3 |
| 2 |
故选：D
点评：本题考查的知识点是由三视图求体积，其中根据已知中的三视图分析出几何体的形状是解答的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}共有11项，a1=0，a11=4，且|ak+1-ak|=1（k=1，2，…，10），则满足该条件的不同数列的个数为（ ）
| A、100 | B、120 |
| C、140 | D、160 |
若函数f（x）为偶函数，x＞0时，f（x）递增，P=f（-π），Q=f（e），R=f（lnπ），则（ ）
| A、P＞Q＞R |
| B、R＞Q＞P |
| C、P＞R＞Q |
| D、Q＞R＞P |
复数
的共轭复数是（ ）
| 1+2i |
| i |
| A、2+i | B、1+2i |
| C、2-i | D、-2+i |
| 2sin40°-cos10° |
| sin10° |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
有一个正方体的玩具，六个面标注了数字1，2，3，4，5，6，甲、乙两位学生进行如下游戏：甲先抛掷一次，记下正方体朝上的数字为a，再由乙抛掷一次，朝上数字为b，若|a-b|≤1就称甲、乙两人“默契配合”，则甲、乙两人“默契配合”的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设
，
为两个非零向量，则“
•
=|
•
|”是“
与
共线”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
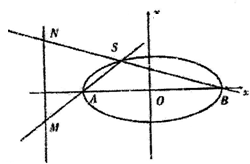如图，已知椭圆C：
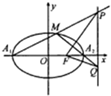如图，A1（-2，0），A2（2，0）是椭圆C：