题目内容
集合A={x|2x-x2>0},B={x|1≤x<2},则∁AB=( )
| A、(0,1) |
| B、(0,1] |
| C、[0,1] |
| D、(1,2) |
考点:补集及其运算
专题:集合
分析:求出集合A,利用集合的基本运算即可得到结论.
解答:
解:A={x|2x-x2>0}={x|0<x<2},B={x|1≤x<2},
∴∁AB={x|0<x<1},
故选:A.
∴∁AB={x|0<x<1},
故选:A.
点评:本题主要考查集合的基本运算,比较基础.

练习册系列答案
相关题目
已知全集U=R,集合A={x|y=log2(-x2+2x)},B={y|y≥1},则A∩∁UB=( )
| A、{x|0<x<1} |
| B、{x|x<0} |
| C、{x|x>2} |
| D、{x|1<x<2} |
一个几何体的三视图如图所示,这个几何体的体积是( )
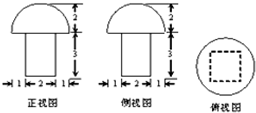

A、
| ||
B、
| ||
C、12+
| ||
D、3+
|
复数Z=(2cosθ-i)(2sinθ+i)为纯虚数,则θ可能取值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}共有11项,a1=0,a11=4,且|ak+1-ak|=1(k=1,2,…,10),则满足该条件的不同数列的个数为( )
| A、100 | B、120 |
| C、140 | D、160 |
若函数f(x)为偶函数,x>0时,f(x)递增,P=f(-π),Q=f(e),R=f(lnπ),则( )
| A、P>Q>R |
| B、R>Q>P |
| C、P>R>Q |
| D、Q>R>P |