题目内容
给出下列四个结论:
①若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0;
②“(x-3)(x-4)=0”是“x-3=0”的充分而不必要条件;
③若a>0,b>0,a+b=4,则
+
的最小值为1.
其中正确结论的个数为( )
①若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0;
②“(x-3)(x-4)=0”是“x-3=0”的充分而不必要条件;
③若a>0,b>0,a+b=4,则
| 1 |
| a |
| 1 |
| b |
其中正确结论的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:由含有一个量词的命题的否定形式,即可判断①;运用充分必要条件的定义,可判断②;将1=
(a+b)代入所求式子,变形后运用基本不等式求出最值,注意等号成立的条件.
| 1 |
| 4 |
解答:
解:①若命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0,故①正确;
②(x-3)(x-4)=0?x=3或x=4,故“(x-3)(x-4)=0”是“x-3=0”的必要不充分条件,故②错;
③若a>0,b>0,a+b=4,则
+
=
(
+
)=
(2+
+
)≥
×(2+2)=1,当且仅当a=b=2取最小值1,故③正确.
故选C.
②(x-3)(x-4)=0?x=3或x=4,故“(x-3)(x-4)=0”是“x-3=0”的必要不充分条件,故②错;
③若a>0,b>0,a+b=4,则
| 1 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| a+b |
| a |
| a+b |
| b |
| 1 |
| 4 |
| b |
| a |
| a |
| b |
| 1 |
| 4 |
故选C.
点评:本题主要考查命题的否定和充分必要条件的判断,同时考查基本不等式及运用求最值,注意等号成立的条件.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
复数Z=(2cosθ-i)(2sinθ+i)为纯虚数,则θ可能取值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}共有11项,a1=0,a11=4,且|ak+1-ak|=1(k=1,2,…,10),则满足该条件的不同数列的个数为( )
| A、100 | B、120 |
| C、140 | D、160 |
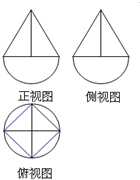 某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设实数x,y满足不等式组
,则z=x-2y的最小值是( )
|
| A、-8 | ||
| B、-6 | ||
| C、-3 | ||
D、-
|
复数
在复平面内所对应的点在实轴上,那么实数a=( )
| a+i |
| 2-i |
| A、-2 | B、0 | C、1 | D、2 |
若函数f(x)为偶函数,x>0时,f(x)递增,P=f(-π),Q=f(e),R=f(lnπ),则( )
| A、P>Q>R |
| B、R>Q>P |
| C、P>R>Q |
| D、Q>R>P |
设
,
为两个非零向量,则“
•
=|
•
|”是“
与
共线”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |