题目内容
已知θ∈(
,π),sinθ=
,求cosθ及sin(θ+
)的值.
| π |
| 2 |
| 4 |
| 5 |
| π |
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系求得cosθ,再利用两角和的正弦公式求得sin(θ+
)的值.
| π |
| 3 |
解答:
解:∵θ∈(
,π),sinθ=
,
∴cosθ=-
=-
.
又∵sin(θ+
)=sinθ•cos
+cosθ•sin
=
cosθ+
sinθ,
∴sin(θ+
)=
×
+
×(-
)=
.
| π |
| 2 |
| 4 |
| 5 |
∴cosθ=-
| 1-sin2θ |
| 3 |
| 5 |
又∵sin(θ+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴sin(θ+
| π |
| 3 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
4-3
| ||
| 10 |
点评:本题主要考查同角三角函数的基本关系,两角和的正弦公式的应用,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
设全集U=R,集合A={x|x2-1<0},B={x|x(x-2)≥0},则A∩(∁UB)=( )
| A、{x|0<x<2} |
| B、{x|0<x<1} |
| C、{x|0≤x<1} |
| D、{x|-1<x<0} |
现有10个数,它们能构成一个以1为首项,-3为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
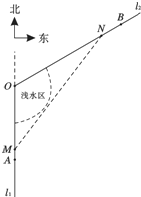 某港湾的平面示意图如图所示,O,A,B分别是海岸线l1,l2上的三个集镇,A位于O的正南方向6km处,B位于O的北偏东60°方向10km处.
某港湾的平面示意图如图所示,O,A,B分别是海岸线l1,l2上的三个集镇,A位于O的正南方向6km处,B位于O的北偏东60°方向10km处.