题目内容
已知函数f(x)=
ax2-(a+1)x+lnx,g(x)=x2-2bx-
.
(Ⅰ)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a<0时,求函数f(x)的单调区间;
(Ⅲ)当a=
时,对任意x1∈(0,2],存在x2∈[1,2],使得f(x1)≤g(x2)成立,求实数b的取值范围.
| 1 |
| 2 |
| 5 |
| 4 |
(Ⅰ)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a<0时,求函数f(x)的单调区间;
(Ⅲ)当a=
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导函数,取得切线的斜率与切点的坐标,即可求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当a<0时,求出函数f(x)的导函数,在定义域下令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间;
(Ⅲ)对任意x1∈(0,2],存在x2∈[1,2],使得f(x1)≤g(x2)成立,等价于f(x)min≤g(x)min,分类讨论,即可求实数b的取值范围.
(Ⅱ)当a<0时,求出函数f(x)的导函数,在定义域下令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间;
(Ⅲ)对任意x1∈(0,2],存在x2∈[1,2],使得f(x1)≤g(x2)成立,等价于f(x)min≤g(x)min,分类讨论,即可求实数b的取值范围.
解答:
解:(Ⅰ)当a=0时,f(x)=-x+lnx,
∴f′(x)=-1+
,f(1)=-1,
∴f′(x)=0
∴曲线y=f(x)在点(1,f(1))处的切线方程为y=-1;
(Ⅱ)∵f(x)=
ax2-(a+1)x+lnx,
∴f′(x)=ax-(a+1)+
=
当a<0时,f′(x)>0,可得x>1;f′(x)<0,可得0<x<1,
∴当a<0时,函数f(x)的单调增区间为(1,+∞),单调减区间为(0,1);
(Ⅲ)当a=
时,f(x)=
x2-
x+lnx,则f′(x)=
x+
-
,
∵x∈(0,2],∴f′(x)=
x+
-
≥
-
,
∴f(x)min=
-
,g(x)=x2-2bx-
=(x-b)2-b2-
∵x∈[1,2],∴b>2时,g(x)min=g(2)=
-4b;1≤b≤2时,g(x)min=b2-
;b<2时,g(x)min=g(1)=-
-2b,
∵对任意x1∈(0,2],存在x2∈[1,2],使得f(x1)≤g(x2)成立,
∴b>2时,
-
≤
-4b,不成立;1≤b≤2时,
-
≤b2-
,∴1≤b≤2;
b<2时,
-
≤-
-2b,∴b≤
-
.
∴b≤
-
或1≤b≤2.
∴f′(x)=-1+
| 1 |
| x |
∴f′(x)=0
∴曲线y=f(x)在点(1,f(1))处的切线方程为y=-1;
(Ⅱ)∵f(x)=
| 1 |
| 2 |
∴f′(x)=ax-(a+1)+
| 1 |
| x |
| (ax-1)(x-1) |
| x |
当a<0时,f′(x)>0,可得x>1;f′(x)<0,可得0<x<1,
∴当a<0时,函数f(x)的单调增区间为(1,+∞),单调减区间为(0,1);
(Ⅲ)当a=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
∵x∈(0,2],∴f′(x)=
| 1 |
| 2 |
| 1 |
| x |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
∴f(x)min=
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
∵x∈[1,2],∴b>2时,g(x)min=g(2)=
| 11 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
∵对任意x1∈(0,2],存在x2∈[1,2],使得f(x1)≤g(x2)成立,
∴b>2时,
| 2 |
| 3 |
| 2 |
| 11 |
| 4 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
b<2时,
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 5 |
| 8 |
| ||
| 2 |
∴b≤
| 5 |
| 8 |
| ||
| 2 |
点评:本小题主要考查函数、函数与导数等基础知识,考查推理论证能力,运算求解能力,考查函数与方程的思想,数形结合的思想,化归与转化思想.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
已知函数f(x)=2x+x,g(x)=log3x+x,h(x)=x-
的零点依次为a,b,c,则( )
| 1 | ||
|
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
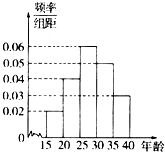 山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表:
山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表: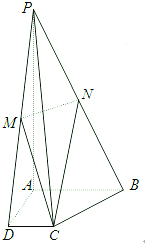 如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
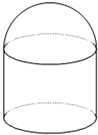 如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.