��Ŀ����
��֪��ԲC��
+
=1��a��b��0�����϶���ΪB2���ҽ���ΪF2����B2OF2Ϊ����ֱ�������Σ�OΪ����ԭ�㣩��������y2=4
x�Ľ���ǡ���Ǹ���Բ���Ҷ��㣮
��1������ԲC�ķ��̣�
��2������B1��B2�ֱ�����Բ���¶�����϶��㣬��P����Բ������B1��B2�ĵ㣬��֤��ֱ��PB1��ֱ��PB2��б��֮��Ϊ��ֵ��
��3����֪ԲM��x2+y2=
������l����Բ�ཻ��C��D���㣬��ô��CDΪֱ����Բ�Ƿ����㣿����ǣ������������ꣻ������ǣ���˵�����ɣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
��1������ԲC�ķ��̣�
��2������B1��B2�ֱ�����Բ���¶�����϶��㣬��P����Բ������B1��B2�ĵ㣬��֤��ֱ��PB1��ֱ��PB2��б��֮��Ϊ��ֵ��
��3����֪ԲM��x2+y2=
| 2 |
| 3 |
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺�ۺ���,Բ���ߵĶ��塢�����뷽��
��������1����֪b=c��a=
����b=c=1��������ԲC�ķ��̣�
��2����P��m��n������
+n2=1�����ֱ��PB1��ֱ��PB2��б�ʣ����ɵó����ۣ�
��3�������ֱ��l��б�ʲ����ڼ�б��Ϊ0ʱԲ�ķ��̣��ɴ˿ɵ���Բ����������Ϊԭ��O����ֱ��l��б�ʴ����Ҳ�Ϊ��ʱ����ֱ��l�ķ���Ϊy=kx+m��������Բ��������y��x�Ķ��η��̣���A��x1��y1����B��x2��y2������Τ�ﶨ���������������ɵ�
•
�ı���ʽ���ٸ�����Բ���пɵ�k��m�Ĺ�ϵʽ��������������ʽ�����
•
=0���ɴ˿ɵý��ۣ�
| 2 |
��2����P��m��n������
| m2 |
| 2 |
��3�������ֱ��l��б�ʲ����ڼ�б��Ϊ0ʱԲ�ķ��̣��ɴ˿ɵ���Բ����������Ϊԭ��O����ֱ��l��б�ʴ����Ҳ�Ϊ��ʱ����ֱ��l�ķ���Ϊy=kx+m��������Բ��������y��x�Ķ��η��̣���A��x1��y1����B��x2��y2������Τ�ﶨ���������������ɵ�
| OA |
| OB |
| OA |
| OB |
���
�⣺��1����֪b=c��a=
��
��b=c=1��
��������
+y2=1��
��2������֪B1��0��-1����B2��0��1����
��P��m��n������
+n2=1��
��kPB1•kPB2=
•
=
=-
��
��3����i����ֱ��l��б�ʲ�����ʱ��
��Ϊֱ��l��ԲM���У������е�һ�����߷���Ϊx=
��
������Բ���̿ɵã��ɵ�A��
��
����B��
��-
����
����ABΪֱ����Բ�ķ���Ϊ��x-
��2+y2=
��
��ii����ֱ��l��б��Ϊ��ʱ��
��Ϊֱ��l��ԲM���У��������е�һ�����߷���Ϊy=-
��
������Բ���̿ɵã��ɵ�A��
��-
����B��-
��-
����
����ABΪֱ����Բ�ķ���Ϊx2+��y+
��2+y2=
��
��Ȼ������Բ��������O��0��0����
��iii����ֱ��l��б�ʴ����Ҳ�Ϊ��ʱ����ֱ��l�ķ���Ϊy=kx+m��
������Բ������ȥy���ã�2k2+1��x2+4kmx+2m2-2=0��
��A��x1��y1����B��x2��y2������x1+x2=
��x1x2=
��
����y1y2=��kx1+m����kx2+m��=k2x1x2+km��x1+x2��+m2=
��
����
•
=x1x2+y1y2=
�٣�
��Ϊֱ��l��ԲM���У�
����Բ�ĵ�ֱ��l�ľ���d=
=
����������m2=
��1+k2������
���ڴ���٣���
•
=����Ȼ��ABΪֱ����Բ��������O��0��0����
���Ͽ�֪����ABΪֱ����Բ�����㣨0��0����
| 2 |
��b=c=1��
��������
| x2 |
| 2 |
��2������֪B1��0��-1����B2��0��1����
��P��m��n������
| m2 |
| 2 |
��kPB1•kPB2=
| n+1 |
| m |
| n-1 |
| m |
| n2-1 |
| m2 |
| 1 |
| 2 |
��3����i����ֱ��l��б�ʲ�����ʱ��
��Ϊֱ��l��ԲM���У������е�һ�����߷���Ϊx=
| ||
| 3 |
������Բ���̿ɵã��ɵ�A��
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
����ABΪֱ����Բ�ķ���Ϊ��x-
| ||
| 3 |
| 2 |
| 3 |
��ii����ֱ��l��б��Ϊ��ʱ��
��Ϊֱ��l��ԲM���У��������е�һ�����߷���Ϊy=-
| ||
| 3 |
������Բ���̿ɵã��ɵ�A��
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
����ABΪֱ����Բ�ķ���Ϊx2+��y+
| ||
| 3 |
| 2 |
| 3 |
��Ȼ������Բ��������O��0��0����
��iii����ֱ��l��б�ʴ����Ҳ�Ϊ��ʱ����ֱ��l�ķ���Ϊy=kx+m��
������Բ������ȥy���ã�2k2+1��x2+4kmx+2m2-2=0��
��A��x1��y1����B��x2��y2������x1+x2=
| -4km |
| 2k2+1 |
| 2m2-2 |
| 2k2+1 |
����y1y2=��kx1+m����kx2+m��=k2x1x2+km��x1+x2��+m2=
| m2-2k2 |
| 2k2+1 |
����
| OA |
| OB |
| 3m2-2k2-2 |
| 2k2+1 |
��Ϊֱ��l��ԲM���У�
����Բ�ĵ�ֱ��l�ľ���d=
| |m| | ||
|
| ||
| 3 |
| 2 |
| 3 |
���ڴ���٣���
| OA |
| OB |
���Ͽ�֪����ABΪֱ����Բ�����㣨0��0����
���������⿼����Բ�ķ��̡�Բ�ķ��̼�ֱ������Բ��λ�ù�ϵ���������������������㣬����ѧ����������������

��ϰ��ϵ�д�
 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
�����Ŀ
���ڶ�����R�ϵĺ���f��x���������ĸ������д������ ��������
| A����f��x�����溯������f��x-2����ͼ����ڵ�A��2��0���Գ� |
| B��������f��x-2����ͼ�����ֱ��x=2�Գƣ���f��x��Ϊż���� |
| C������x��R����f��x-2��=-f��x������4��f��x�������� |
| D������y=f��x-2����y=f��2-x����ͼ�����ֱ��x=0�Գ� |
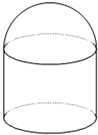 ��ͼ������ı����SΪ��ֵ�������ϲ��ǰ����²���Բ��������İ뾶����Բ������뾶��
��ͼ������ı����SΪ��ֵ�������ϲ��ǰ����²���Բ��������İ뾶����Բ������뾶�� ��֪��ԲE��
��֪��ԲE�� ��ͼ��ƽ��ABB1A1ΪԲ��OO1������棬��CΪ
��ͼ��ƽ��ABB1A1ΪԲ��OO1������棬��CΪ