题目内容
已知椭圆C:
+
=1(a<b<0)的离心率为
,椭圆C的中心O关于直线2x-y-5=0的对称点落在直线x=a2上.
(1)求椭圆C的方程;
(2)设P(4,0)是椭圆C上关于x轴对称的任意两点,连接PN交椭圆C于另一点E,求直线PN的斜率范围并证明直线ME与x轴相交顶点.
| x2 |
| a2 |
| r2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)设P(4,0)是椭圆C上关于x轴对称的任意两点,连接PN交椭圆C于另一点E,求直线PN的斜率范围并证明直线ME与x轴相交顶点.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由题意知e=
=
,则a=2c,求出椭圆C的中心O关于直线2x-y-5=0的对称点,可求a,即可得出椭圆C的方程;
(2)设直线PN的方程为y=k(x-4)代入椭圆方程,根据判别式,可求直线PN的斜率范围,求出直线ME的方程为y-y2=
(x-x2),令y=0,得x=x2-
,即可得出结论.
| c |
| a |
| 1 |
| 2 |
(2)设直线PN的方程为y=k(x-4)代入椭圆方程,根据判别式,可求直线PN的斜率范围,求出直线ME的方程为y-y2=
| y2+y1 |
| x2-x1 |
| y2(x2-x1) |
| y2+y1 |
解答:
解:(1)由题意知e=
=
,则a=2c,
设椭圆C的中心O关于直线2x-y-5=0的对称点(m,n),则
,
∴m=4,n=-2,
∵椭圆C的中心O关于直线2x-y-5=0的对称点落在直线x=a2上.
∴a2=4,∴c=1,
∴b=
,
∴椭圆C的方程为
+
=1;
(2)由题意知直线PN的斜率存在,设直线PN的方程为y=k(x-4).
代入椭圆方程,可得(4k2+3)x2-32k2x+64k2-12=0.①
由△=(-32k2)2-4(4k2+3)(64k2-12)>0,得4k2-1<0,∴-
<k<
又k=0不合题意,∴直线PN的斜率的取值范围是:(-
,0)∪(0,
).
(Ⅲ)设点N(x1,y1),E(x2,y2),则M(x1,-y1).
直线ME的方程为y-y2=
(x-x2).
令y=0,得x=x2-
.
将y1=k(x1-4),y2=k(x2-4)代入整理,得x=
.②
由①得x1+x2=
,x1x2=
代入②整理,得x=1.
∴直线ME与x轴相交于定点(1,0).
| c |
| a |
| 1 |
| 2 |
设椭圆C的中心O关于直线2x-y-5=0的对称点(m,n),则
|
∴m=4,n=-2,
∵椭圆C的中心O关于直线2x-y-5=0的对称点落在直线x=a2上.
∴a2=4,∴c=1,
∴b=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由题意知直线PN的斜率存在,设直线PN的方程为y=k(x-4).
代入椭圆方程,可得(4k2+3)x2-32k2x+64k2-12=0.①
由△=(-32k2)2-4(4k2+3)(64k2-12)>0,得4k2-1<0,∴-
| ||
| 6 |
| ||
| 6 |
又k=0不合题意,∴直线PN的斜率的取值范围是:(-
| ||
| 6 |
| ||
| 6 |
(Ⅲ)设点N(x1,y1),E(x2,y2),则M(x1,-y1).
直线ME的方程为y-y2=
| y2+y1 |
| x2-x1 |
令y=0,得x=x2-
| y2(x2-x1) |
| y2+y1 |
将y1=k(x1-4),y2=k(x2-4)代入整理,得x=
| 2x1x2-4(x1+x2) |
| x1+x2-8 |
由①得x1+x2=
| 32k2 |
| 4k2+3 |
| 64k2-12 |
| 4k2+3 |
代入②整理,得x=1.
∴直线ME与x轴相交于定点(1,0).
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
各项均为实数的等比数列{an}中,a1=1,a5=4,则a3=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
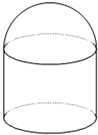 如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径. 已知椭圆E:
已知椭圆E: 如图,平面ABB1A1为圆柱OO1的轴截面,点C为
如图,平面ABB1A1为圆柱OO1的轴截面,点C为