题目内容
(1)当x=x0时,函数f(x)=
取得最大值,则cos2x0的值为( )
| cosx | ||||
sin4
|
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、1 |
考点:三角函数的最值
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:运用同角的平方关系和二倍角的正弦公式和余弦公式,化简f(x),再由余弦函数的值域即可最大值和对应的x的值,进而求得结论.
解答:
解:函数f(x)=
=
=
=
=
=4-
,
由于-1≤cosx≤1,则2≤3+cosx≤4,
则当cosx=1,即x=2kπ,k∈Z时,f(x)取得最大值,且为1.
则有cos2x0=cos4kπ=1.
故选D.
| cosx | ||||
sin4
|
| cosx | ||||||||
(cos2
|
=
| cosx | ||||
1-
|
| 2cosx | ||
2-
|
| 4cosx |
| 3+cosx |
| 12 |
| 3+cosx |
由于-1≤cosx≤1,则2≤3+cosx≤4,
则当cosx=1,即x=2kπ,k∈Z时,f(x)取得最大值,且为1.
则有cos2x0=cos4kπ=1.
故选D.
点评:本题考查三角函数的化简和求值,考查二倍角公式和余弦函数的值域,考查运算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知|
|=1,|
|=2,
与
的夹角为60°,则
+
在
方向上的投影为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、2 | ||||
| B、1 | ||||
C、
| ||||
D、
|
命题P:函数f(x)=(
)x-sinx至少有两个零点,对于命题P的否定,下列说法正确的是( )
| 1 |
| 3 |
A、命题P的否定:函数f(x)=(
| ||
B、命题P的否定:函数f(x)=(
| ||
C、命题P的否定:函数f(x)=(
| ||
D、命题P的否定:函数f(x)=(
|
已知双曲线
-
=1(a>0,b>0)的右顶点和右焦点分别为A(a,0)、F(c,0),若直线x=
上存在点P使得∠APF=30°,则刻双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
A、(1,
| ||||
B、[
| ||||
| C、(1,2] | ||||
| D、[2,+∞) |
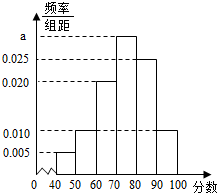 从某校高三年级学生中抽取40名学生,将他们高中学业水平考试的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
从某校高三年级学生中抽取40名学生,将他们高中学业水平考试的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.