题目内容
 椭圆C的中心在原点,焦点在x轴上,离心率为
椭圆C的中心在原点,焦点在x轴上,离心率为
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
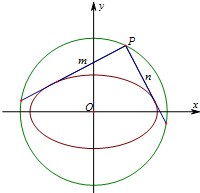
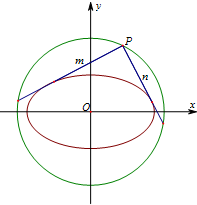
(Ⅱ)如图,过圆D:x2+y2=4上任意一点P作椭圆C的两条切线m,n. 求证:m⊥n.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)通过离心率得到a、b关系式,设出椭圆C的方程,利用直线y=x+2与椭圆相切,△=0.由此得b2=1;求出椭圆方程即可.
(Ⅱ)设P(x0,y0).当x0=±
时,有一条切线斜率不存在,证明m⊥n.
设x0≠±
,则两条切线斜率存在.设直线m的斜率为k,则其方程为y-y0=k(x-x0),联立
+y2=1,由△=0可得:(3-
)k2+2x0y0k+1-
=0,由韦达定理得到k1k2=
,由于点P在圆D:x2+y2=4上,得到3-
=-(1-
),即可证明m⊥n.
(Ⅱ)设P(x0,y0).当x0=±
| 3 |
设x0≠±
| 3 |
| x2 |
| 3 |
| x | 2 0 |
| y | 2 0 |
1-
| ||
3-
|
| x | 2 0 |
| y | 2 0 |
解答:
 解:(Ⅰ)由e=
解:(Ⅰ)由e=
知a2=3b2,
椭圆方程可设为
+
=1.又直线y=x+2与椭圆相切,代入后方程4x2+12x+12-3b2=0满足△=0.由此得b2=1.
故椭圆C的方程为
+y2=1.----------------(6分)
(Ⅱ)设P(x0,y0).当x0=±
时,有一条切线斜率不存在,此时,刚好y0=±1,可见,另一条切线平行于x轴,m⊥n;----------------(7分)
设x0≠±
,则两条切线斜率存在.设直线m的斜率为k,则其方程为y-y0=k(x-x0)
即y=kx+y0-kx0.代入
+y2=1并整理得:(1+3k2)x2+6k(y0-kx0)x+3(y0-kx0)2-3=0.---------------(9分)
由△=0可得:(3-
)k2+2x0y0k+1-
=0---------------(11分)
注意到直线n的斜率也适合这个关系,所以m,n的斜率k1,k2就是上述方程的两根,由韦达定理,k1k2=
.---------------(13分)
由于点P在圆D:x2+y2=4上,3-
=-(1-
),所以k1k2=-1.这就证明了m⊥n.
综上所述,过圆D上任意一点P作椭圆C的两条切线m,n,总有m⊥n.------(15分)
 解:(Ⅰ)由e=
解:(Ⅰ)由e=
| ||
| 3 |
椭圆方程可设为
| x2 |
| 3b2 |
| y2 |
| b2 |
故椭圆C的方程为
| x2 |
| 3 |
(Ⅱ)设P(x0,y0).当x0=±
| 3 |
设x0≠±
| 3 |
即y=kx+y0-kx0.代入
| x2 |
| 3 |
由△=0可得:(3-
| x | 2 0 |
| y | 2 0 |
注意到直线n的斜率也适合这个关系,所以m,n的斜率k1,k2就是上述方程的两根,由韦达定理,k1k2=
1-
| ||
3-
|
由于点P在圆D:x2+y2=4上,3-
| x | 2 0 |
| y | 2 0 |
综上所述,过圆D上任意一点P作椭圆C的两条切线m,n,总有m⊥n.------(15分)
点评:本题考查椭圆方程的求法,直线与圆的位置关系,直线与椭圆方程的综合应用,考查分析问题解决问题的能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
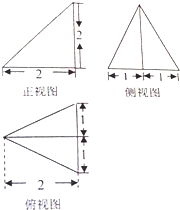
已知某个几何体的三视图如右图,根据图中标出的尺寸可得这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
若方程|2x-2|-a=0有两个解,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,2) | D、∅ |
设a>0,且a≠1,且a≠2,则“函数y=logax在(0,+∞)上是减函数”是“函数y=(a-2)ax在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,若其图象向右平移
个单位后关于y轴对称,则y=f(x)对应的解析式为 ( )
| π |
| 2 |
| π |
| 3 |
A、y=sin(2x-
| ||
B、y=cos(2x+
| ||
C、y=cos(2x-
| ||
D、y=sin(2x+
|