题目内容
已知函数f(x)=2x3+ax2+bx-26(a,b∈R)在x=-3和x=2处取到极值.
(1)求a,b和f(-3)-f(2)的值;
(2)求最大的正整数t,使得?x1,x2∈[-t,t]时,|f(x1)-f(x2)|≤125与|f′(x1)-f′(x2)|≤125同时成立.
(1)求a,b和f(-3)-f(2)的值;
(2)求最大的正整数t,使得?x1,x2∈[-t,t]时,|f(x1)-f(x2)|≤125与|f′(x1)-f′(x2)|≤125同时成立.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)求导数f′(x),由题意得f′(-3)=0,f′(2)=0,解方程组即可求得a,b值,
代入求得f(-3)-f(2),
(2)先求出得?x1,x2∈[-t,t]时,|f(x1)-f(x2)|≤125的t的最大值,再求出?x1,x2∈[-t,t]时,|f′(x1)-f′(x2)|≤125的最大值,问题得解决.
代入求得f(-3)-f(2),
(2)先求出得?x1,x2∈[-t,t]时,|f(x1)-f(x2)|≤125的t的最大值,再求出?x1,x2∈[-t,t]时,|f′(x1)-f′(x2)|≤125的最大值,问题得解决.
解答:
解:(1)f′(x)=6x2+2ax+b,
因为函数f(x)在x=-1和x=3时取得极值,
所以
,即
解得a=3,b=-36,
∴f(x)=2x3+3x2-36x-26,
∴f(-3)=55,f(2)=-70
∴f(-3)-f(2)=125.
(2)由(1)知,f′(x)=6x2+6ax-36=6(x+3)(x-2)=6(x+
)2-
,
∵f′(x)=0的两个根为-3和2,
∴f(x)在(-∞,-3)和(2,+∞)上单调递增,在(-3,2)上单调递减,
∴当x=-3时f(x)取得极大值,当x=2时f(x)取得极小值,
∴|f(-3)-f(2)|=125.
令f(x)=2x3+3x2-36x-26=55,
∴2x3+3x2-36x-81=0,
其有一个根为-3,则分解得:(x+3)2•(2x-9)=0,
解得x=-3或x=
,
令f(x)=2x3+3x2-36x-26=-70,
∴2x3+3x2-36x+44=0,
其有一个根为3,则分解得:(x-2)2•(2x+11)=0,
解得x=2或x=-
,
则要使得?x1,x2∈[-t,t]时|f(x1)-f(x2)|≤125,必须满足0<t≤
,
∵t为正整数,
∴t最大为4.
另一方面,f′(x)=6x2+6ax-36=6(x+
)2-
,
由于t∈Z,要使得?x1,x2∈[-t,t]时|f′(x1)-f′(x2)|≤125成立,
则f′(t)-(-
)≤125,
即6t2+6t-36-(-
)≤125,
∴12t2+12t-247≤0,
令g(t)=12t2+12t-247,
则g(4)=-7<0,g(5)=113>0,
要使得?x1,x2∈[-t,t]时|f′(x1)-f′(x2)|≤125成立,
t≤4,
综上所述,最大的正整数t为4.
因为函数f(x)在x=-1和x=3时取得极值,
所以
|
|
∴f(x)=2x3+3x2-36x-26,
∴f(-3)=55,f(2)=-70
∴f(-3)-f(2)=125.
(2)由(1)知,f′(x)=6x2+6ax-36=6(x+3)(x-2)=6(x+
| 1 |
| 2 |
| 75 |
| 2 |
∵f′(x)=0的两个根为-3和2,
∴f(x)在(-∞,-3)和(2,+∞)上单调递增,在(-3,2)上单调递减,
∴当x=-3时f(x)取得极大值,当x=2时f(x)取得极小值,
∴|f(-3)-f(2)|=125.
令f(x)=2x3+3x2-36x-26=55,
∴2x3+3x2-36x-81=0,
其有一个根为-3,则分解得:(x+3)2•(2x-9)=0,
解得x=-3或x=
| 9 |
| 2 |
令f(x)=2x3+3x2-36x-26=-70,
∴2x3+3x2-36x+44=0,
其有一个根为3,则分解得:(x-2)2•(2x+11)=0,
解得x=2或x=-
| 11 |
| 2 |
则要使得?x1,x2∈[-t,t]时|f(x1)-f(x2)|≤125,必须满足0<t≤
| 9 |
| 2 |
∵t为正整数,
∴t最大为4.
另一方面,f′(x)=6x2+6ax-36=6(x+
| 1 |
| 2 |
| 75 |
| 2 |
由于t∈Z,要使得?x1,x2∈[-t,t]时|f′(x1)-f′(x2)|≤125成立,
则f′(t)-(-
| 75 |
| 2 |
即6t2+6t-36-(-
| 75 |
| 2 |
∴12t2+12t-247≤0,
令g(t)=12t2+12t-247,
则g(4)=-7<0,g(5)=113>0,
要使得?x1,x2∈[-t,t]时|f′(x1)-f′(x2)|≤125成立,
t≤4,
综上所述,最大的正整数t为4.
点评:本题考查利用导数研究函数的极值及求函数在闭区间上的最值问题,考查函数恒成立问题,考查学生对问题的转化能力,恒成立问题往往转化为函数最值解决,属于难题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知f(x)=
,则f(-1)+f(4)的值是( )
|
| A、-7 | B、3 | C、-8 | D、4 |
在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
已知f(x)=2x+3(x∈R),若|f(x)|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
A、b≥
| ||
B、b<
| ||
C、a≤
| ||
D、a>
|
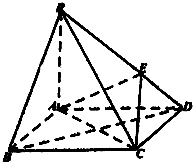 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=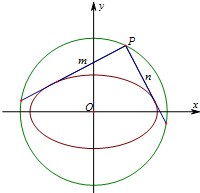 椭圆C的中心在原点,焦点在x轴上,离心率为
椭圆C的中心在原点,焦点在x轴上,离心率为