题目内容

若方程|2x-2|-a=0有两个解，则a的取值范围是（　　）
A、（1，+∞）B、（0，1）
C、（0，2）D、∅
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由题意可得函数y=|2x-2|的图象和直线y=a有2个交点，数形结合可得a的范围．
解答： 解：∵方程|2x-2|-a=0有两个解，∴函数y=|2x-2|的图象和直线y=a有2个交点，
如图所示：
则a的取值范围是0＜a＜2，
故选：C．
点评：本题主要考查方程的根的存在性及个数判断，体现了化归与转化、数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
已知定义在R上的函数f（x）=
(5-m)x+1，(x≤0)
mx+m-1，(x＞0)
，若f（x）在（-∞，+∞）上单调递增，则实数m的取值范围是
 
．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，且该椭圆上一点A与左、右焦点F1，F2构成的三角形周长为2
2
+2．
（Ⅰ）求椭圆C的方程；
（Ⅱ）记椭圆C的上顶点为B，直线l交椭圆C于P，Q两点，问：是否存在直线l，使椭圆C的右焦点F2恰为△PQB的垂心（△PQB三条边上的高线的交点）？若存在，求出直线l的方程，若不存在，请说明理由．
（Ⅲ）若⊙M是以AF2为直径的圆，求证：⊙M与以坐标原点为圆心，a为半径的圆相内切．
如图，菱形ABCD与矩形BDEF所在平面互相垂直，∠BAD=
π
3
．
（Ⅰ）求证：FC∥平面AED；
（Ⅱ）若BF=k•BD，当二面角A-EF-C为直二面角时，求k的值；
（Ⅲ）在（Ⅱ）的条件下，求直线BC与平面AEF所成的角θ的正弦值．
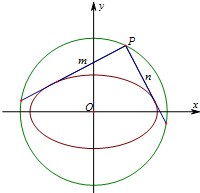椭圆C的中心在原点，焦点在x轴上，离心率为
6
3
，并与直线y=x+2相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）如图，过圆D：x2+y2=4上任意一点P作椭圆C的两条切线m，n． 求证：m⊥n．
已知：抛物线y=ax2+（1-a）x+3（a≠0）在（-∞，2]上单调递增，求a的范围．
构造如图所示的数表，规则如下：先排两个l作为第一层，然后在每一层的相邻两个数之间插入这两个数和的a倍得下一层，其中a∈（0，
1
3
），设第n层中有an个数，这an个数的和为Sn（n∈N*）．
（I）求an；
（Ⅱ）证明：
n
2
≤
a1-1
S1
+
a2-1
S2
+…+
an-1
Sn
＜(
2
a+1
)n-1．
有一小型自来水厂，蓄水池中已有水450吨，水厂每小时可向蓄水池注水80吨，同时蓄水池向居民小区供水，x小时内供水总量为80
20x
吨．现在开始向池中注水并同时向居民小区供水，问：
（1）多少小时后蓄水池中的水量最少？
（2）如果蓄水池中存水量少于150吨时，就会出现供水紧张，那么有几个小时供水紧张？
已知曲线C1，C2的极坐标方程分别为ρ=4cos（θ+
π
6
）和ρcos（θ+
π
6
）=5．
（1）将C1，C2的方程化为直角坐标方程；
（2）设点P在曲线C1上，点Q在C2上，求|PQ|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网