题目内容
19.已知向量$\overrightarrow{a}$=(-3,2),$\overrightarrow{b}$=(2,1),$\overrightarrow{c}$=(3,-1),t∈R,(1)若$\overrightarrow{a}$-t$\overrightarrow{b}$与$\overrightarrow{c}$共线,求实数t的值;
(2)请用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{c}$.
分析 (1)求出$\overrightarrow{a}-t\overrightarrow{b}$的坐标,根据共线定理列方程解出t;
(2)设$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,列方程组解出x,y即可.
解答 解:(1)∵$\overrightarrow{a}-t\overrightarrow{b}$=(-3-2t,2-t),
又$\overrightarrow{a}-t\overrightarrow{b}$与$\overrightarrow{c}$共线,$\overrightarrow{c}$=(3,-1),
∴(-3-2t)×(-1)-(2-t)×3=0,解得t=$\frac{3}{5}$.
(2)设$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x、y∈R),则$\left\{\begin{array}{l}{3=-3x+2y}\\{-1=2x+y}\end{array}\right.$
解得$x=-\frac{5}{7},y=\frac{3}{7},故\overrightarrow c=-\frac{5}{7}\overrightarrow a+\frac{3}{7}\overrightarrow b$.
点评 本题考查了平面向量的基本定理,属于基础题.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
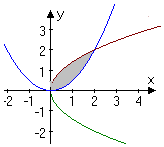 已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.
已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.