题目内容
4.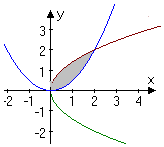 已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.
已知曲线C1:y2=2x与C2:y=$\frac{1}{2}{x^2}$.求两条曲线所围图形(如图所示阴影部分)的面积S.
分析 根据定积分的几何意义计算.
解答 解:解方程组$\left\{\begin{array}{l}{{y}^{2}=2x}\\{y=\frac{1}{2}{x}^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
∴阴影面积S=${∫}_{0}^{2}$($\sqrt{2x}$-$\frac{1}{2}{x}^{2}$)dx=($\frac{2\sqrt{2}}{3}$x${\;}^{\frac{3}{2}}$-$\frac{1}{6}$x3)${|}_{0}^{2}$=$\frac{4}{3}$.
点评 本题考查了定积分在几何中的应用,属于中档题.

练习册系列答案
相关题目
14.设等差数列{an}的前n项和为Sn,若a3=3,Sm=19,Sm+5=14,则m的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
15.用一个平面去截一个几何体,得到的截面是平面四边形,这个几何体不可能是( )
| A. | 三棱锥 | B. | 棱柱 | C. | 四棱台 | D. | 球 |
12.已知点P是圆x2+y2=1上动点,定点Q(6,0),点M是线段PQ靠近Q点的三等分点,则点M的轨迹方程是( )
| A. | (x+3)2+y2=4 | B. | (x-4)2+y2=$\frac{1}{9}$ | C. | (2x-3)2+4y2=1 | D. | (2x+3)2+4y2=1 |
9.已知两点A(2,2),B(2,1),O为坐标原点,若|$\overrightarrow{OA}$-t$\overrightarrow{OB}$|≤$\frac{2\sqrt{5}}{5}$,则实数t的值为( )
| A. | $\frac{6}{5}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{4}{3}$ |