题目内容
9．已知sinα+cosα=$\sqrt{2}$，求sin（α+$\frac{π}{4}$）的值．分析 利用和与差公式求sin（α+$\frac{π}{4}$）求值即可．
解答 解：∵sinα+cosα=$\sqrt{2}$，
那sin（α+$\frac{π}{4}$）=cos$\frac{π}{4}$sinα+sin$\frac{π}{4}$cosα=$\frac{\sqrt{2}}{2}$（sinα+cosα）=1．
点评 本题考查了和与差公式的计算，比较基础．
练习册系列答案
相关题目
4．下列说法中正确的是（ ）
| A． | 当a＞1时，函数y=ax是增函数，因为2＞l，所以函数y=2x是增函数．这种推理是合情推理 | |
| B． | 在平面中，对于三条不同的直线a，b，c，若a∥b，b∥c，则a∥c，将此结论放到空间中也是如此．这种推理是演绎推理 | |
| C． | 若分类变量X与Y的随机变量K2的观测值k越小，则两个分类变量有关系的把握性越小 | |
| D． | $\int_{-1}^1{{x^3}dx=\frac{1}{2}}$ |
5．若二项式${（\sqrt{x}-\frac{1}{x}）^n}$的展开式中，只有第4项的二项式系数最大，则展开式中的常数项是（ ）
| A． | 20 | B． | -20 | C． | 15 | D． | -15 |
4．在直角坐标平面内，如果两点P，Q满足条件：①P，Q都在函数y=f（x）的图象上；②P，Q关于y轴对称，则称（P，Q）是函数y=f（x）的一对“偶点”（偶点（P，Q）与（Q，P）看作同一对偶点），已知函数f（x）=$\left\{\begin{array}{l}{kx-1，x≥0}\\{2{x}^{2}+4x+3，x＜0}\end{array}\right.$有两对“偶点”，则实数k的取值范围是（ ）
| A． | （-∞，-4-4$\sqrt{2}$） | B． | （-4+4$\sqrt{2}$，+∞） | C． | （-4-4$\sqrt{2}$，-4+4$\sqrt{2}$） | D． | （0，-4+4$\sqrt{2}$） |
1．已知圆C1：（x+1）2+（y-1）2=4，圆C2与圆C1关于直线x-y-1=0对称，则圆C2的方程为（ ）
| A． | （x+2）2+（y-2）2=4 | B． | （x-2）2+（y+2）2=4 | C． | （x+2）2+（y+2）2=4 | D． | （x-2）2+（y-2）2=4 |
18．椭圆$\left\{\begin{array}{l}x=5cosφ\\ y=3sinφ\end{array}\right.（φ为参数）$的焦点坐标为（ ）
| A． | （±5，0） | B． | （±4，0） | C． | （±3，0） | D． | （0，±4） |
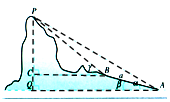如图，在山脚A测得山顶P的仰角为60°，沿倾斜角为15°的斜坡向上走200米到B，在B处测得山顶P的仰角为75°，则山高h=150（$\sqrt{6}$+$\sqrt{2}$）米．