Question

19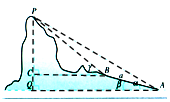．如图，在山脚A测得山顶P的仰角为60°，沿倾斜角为15°的斜坡向上走200米到B，在B处测得山顶P的仰角为75°，则山高h=150（$\sqrt{6}$+$\sqrt{2}$）米．

Answer 1

分析 用h表示出BC，AQ，列方程解出h．

解答 解：CQ=200sin15°=50（$\sqrt{6}$-$\sqrt{2}$），
AQ=$\frac{h}{tan60°}$=$\frac{\sqrt{3}}{3}$h，
BC=$\frac{PC}{tan75°}$=$\frac{h-50（\sqrt{6}-\sqrt{2}）}{2+\sqrt{3}}$=（2-$\sqrt{3}$）h-50（3$\sqrt{6}$-5$\sqrt{2}$），
∴$\frac{\sqrt{3}}{3}$h-（2-$\sqrt{3}$）h+50（3$\sqrt{6}$-5$\sqrt{2}$）=200cos15°=50（$\sqrt{6}$+$\sqrt{2}$），
解得h=150（$\sqrt{6}$+$\sqrt{2}$）．
故答案为：150（$\sqrt{6}$+$\sqrt{2}$）．

点评 本题考查了解三角形的实际应用，属于基础题．