题目内容
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.(1)求证:平面DEC⊥平面BDE;
(2)求点A到平面BDE的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:(1)取DE的中点,连接CH,BH,由等边三角形CDE,可得,CH⊥DE,再通过计算,运用勾股定理的逆定理,得到CH⊥BH,再由线面垂直的判定定理和面面垂直的判定定理,即可得证;
(2)设点A到平面BDE的距离为d,E到平面ABCD的距离为m,由于VA-BDE=VE-ABD,VE-BCD=VC-EBD=
CH•S△BDE,运用三棱锥的体积公式,计算即可得到m,d.
(2)设点A到平面BDE的距离为d,E到平面ABCD的距离为m,由于VA-BDE=VE-ABD,VE-BCD=VC-EBD=
| 1 |
| 3 |
解答:
 (1)证明:取DE的中点,连接CH,BH,
(1)证明:取DE的中点,连接CH,BH,
则由等边三角形CDE,可得,CH⊥DE,
CH=
×6=3
,BD=
=
,
由于BE=7,DE=6,BD=
,有BD2+DE2=BE2,
即有BD⊥DE,
即有BH=
=
,再由BH2+CH2=CB2,
则CH⊥BH,又CH⊥DE,DE,BH为平面BDE中两条相交直线,
则CH⊥平面BDE,且CH?平面CDE,
则平面DEC⊥平面BDE;
(2)解:设点A到平面BDE的距离为d,E到平面ABCD的距离为m,
由于VA-BDE=VE-ABD,
VE-BCD=VC-EBD=
CH•S△BDE=
•3
•
•6
=3
,
又VE-BCD=
•m•
•3•7=3
,
则m=
.
VE-ABD=
m•
•3•2=m,VA-BDE=
d•
•6•
则
d=
,则d=
.
 (1)证明:取DE的中点,连接CH,BH,
(1)证明:取DE的中点,连接CH,BH,则由等边三角形CDE,可得,CH⊥DE,
CH=
| ||
| 2 |
| 3 |
| 22+32 |
| 13 |
由于BE=7,DE=6,BD=
| 13 |
即有BD⊥DE,
即有BH=
(
|
| 22 |
则CH⊥BH,又CH⊥DE,DE,BH为平面BDE中两条相交直线,
则CH⊥平面BDE,且CH?平面CDE,
则平面DEC⊥平面BDE;
(2)解:设点A到平面BDE的距离为d,E到平面ABCD的距离为m,
由于VA-BDE=VE-ABD,
VE-BCD=VC-EBD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
| 13 |
| 39 |
又VE-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 39 |
则m=
6
| ||
| 7 |
VE-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 13 |
则
| 13 |
6
| ||
| 7 |
6
| ||
| 7 |
点评:本题考查面面垂直的判定,考查点到平面的距离的求法,注意运用等积法,考查运算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.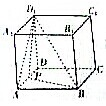 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.