题目内容
某地区预计2015年的前x个月内对某种商品的需求总量f(x)(万件)与月份x的近似关系式是f(x)=
x(x+1)(19-x),x∈N*,1≤x≤12,则2015年的第x月的需求量g(x)(万件)与月份x的函数关系式是 .
| 1 |
| 75 |
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:由题意得,第x个月的需求量等于第x个月的需求总量减去第x-1个月的需求总量,当x=1时,g(1)=f(1);当2≤x≤12时,g(x)=f(x)-f(x-1).
解答:
解:当x=1时,g(1)=f(1)=
.
当2≤x≤12,x∈N*时,g(x)=f(x)-f(x-1)=
x(x+1)(19-x)-
(x-1)x(20-x)
=
x(13-x)
验证x=1符合g(x)=
x(13-x),
∴g(x)=
x(13-x)(x∈N*且x≤12).
故答案为:g(x)=
x(13-x)(x∈N*且x≤12).
| 12 |
| 25 |
当2≤x≤12,x∈N*时,g(x)=f(x)-f(x-1)=
| 1 |
| 75 |
| 1 |
| 75 |
=
| 1 |
| 25 |
验证x=1符合g(x)=
| 1 |
| 25 |
∴g(x)=
| 1 |
| 25 |
故答案为:g(x)=
| 1 |
| 25 |
点评:本题考查利用函数知识解决应用题的有关知识,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列关系中正确的是( )
A、log76<ln
| ||
B、log3π<ln
| ||
C、ln
| ||
D、ln
|
若关于x的方程25-|x+1|-4×5-|x+1|=m有实根,则实数m的取值范围是( )
| A、m<0 | B、m≥-4 |
| C、-4≤m<0 | D、-3≤m<0 |
 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.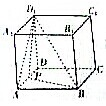 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.