题目内容
设Sn为数列{an}的前n项和,an=1+2+22+…+2n-1,则Sn的值为( )
| A、2n-1 |
| B、2n-1-1 |
| C、2n-n-2 |
| D、2n+1-n-2 |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:运用等比数列的求和公式,求出an,再运用分组求和方法,再由等比数列的求和公式,即可得到结论.
解答:
解:an=1+2+22+…+2n-1
=
=2n-1,
则Sn=(2-1)+(22-1)+…+(2n-1)
=(2+22+…+2n)-n
=
-n=2n+1-2-n.
故选D.
=
| 1-2n |
| 1-2 |
则Sn=(2-1)+(22-1)+…+(2n-1)
=(2+22+…+2n)-n
=
| 2(1-2n) |
| 1-2 |
故选D.
点评:本题考查等比数列的通项和求和公式及运用,考查分组求和的方法,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的方程25-|x+1|-4×5-|x+1|=m有实根,则实数m的取值范围是( )
| A、m<0 | B、m≥-4 |
| C、-4≤m<0 | D、-3≤m<0 |
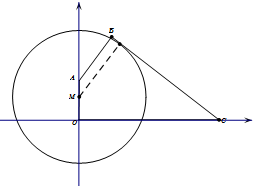 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO= 如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积.
如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积. 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.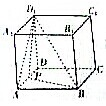 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.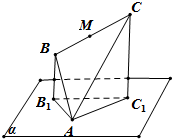 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是