题目内容
在△ABC中角B为钝角,a,b,c分别是角A,B,C的对边,且满足2bsinA=
a.
(1)求角B的值.
(2)若b=19,a+c=5,求a、c的值..
| 3 |
(1)求角B的值.
(2)若b=19,a+c=5,求a、c的值..
考点:余弦定理,正弦定理
专题:集合
分析:(1)已知等式利用正弦定理化简,求出sinB的值,根据B为钝角,求出B的度数即可;
(2)利用余弦定理列出关系式,再利用完全平方公式变形,把各自的值代入求出a与c的值即可.
(2)利用余弦定理列出关系式,再利用完全平方公式变形,把各自的值代入求出a与c的值即可.
解答:
解:(1)已知等式2bsinA=
a,
利用正弦定理化简得:2sinBsinA=
sinA,
∵sinA≠0,∴sinB=
,
∵B为钝角,
∴B=
;
(2)∵b=
,a+c=5,B=
,
∴由余弦定理得:b2=a2+c2-2accosB=(a+c)2-2ac-2accosB,
即19=25-2ac+ac,即ac=6①,
与a+c=5②,
联立①②,解得:a=2,c=3;a=3,c=2.
| 3 |
利用正弦定理化简得:2sinBsinA=
| 3 |
∵sinA≠0,∴sinB=
| ||
| 2 |
∵B为钝角,
∴B=
| 2π |
| 3 |
(2)∵b=
| 19 |
| 2π |
| 3 |
∴由余弦定理得:b2=a2+c2-2accosB=(a+c)2-2ac-2accosB,
即19=25-2ac+ac,即ac=6①,
与a+c=5②,
联立①②,解得:a=2,c=3;a=3,c=2.
点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
已知集合A到B的映射f:x→y=
,则集合A中元素3在B中所对应的元素是( )
| 12 |
| x+1 |
| A、1 | B、2 | C、3 | D、4 |
下列关系中正确的是( )
A、log76<ln
| ||
B、log3π<ln
| ||
C、ln
| ||
D、ln
|
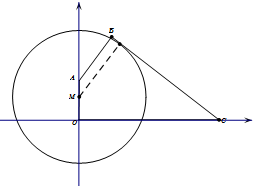 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=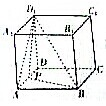 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.